Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Konjugovaná funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 01. 2014 16:36 — Editoval Aquabellla (25. 01. 2014 13:50)
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Konjugovaná funkce
Pěkné odpoledne přeji.
Pro  dokažte, že pro funkci
dokažte, že pro funkci  je konjugovaná funkce:
je konjugovaná funkce:  ,
,
kde  ; funkce
; funkce  ; body
; body  .
.
Definice konjugované funkce: 
Zkoušela jsem použít vztah  , kde
, kde  je funkce duální úlohy,
je funkce duální úlohy,  je funkce závislá na parametru a
je funkce závislá na parametru a  je konjugovaná funkce od funkce závislé na parametru.
je konjugovaná funkce od funkce závislé na parametru. , kde
, kde  je Lagrangeova funkce.
je Lagrangeova funkce.
Dostala jsem se do tvaru:  , ale nejde se mi dostat do konečného výsledku.
, ale nejde se mi dostat do konečného výsledku.
Prosím o jakoukoliv radu, i třeba o jiný postup řešení.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
- (téma jako vyřešené označil(a) Aquabellla)
#3 25. 01. 2014 13:49
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Konjugovaná funkce
↑ Brano:
Samozřejmě, to byl překlep. Děkuji, opravím to.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#4 25. 01. 2014 21:30 — Editoval Brano (25. 01. 2014 21:33)
Re: Konjugovaná funkce
Podla mna je hlavny problem v tom, ze to pises tak dost "barbarsky". (Teda ak som nieco podstatne neprehliadol.)
Standardne sa definuje symbol  pricom ak
pricom ak  tak sa pise bud
tak sa pise bud alebo ekvivalentne
alebo ekvivalentne 
ty pouzivas znacenie vo forme  pricom tym myslis
pricom tym myslis  .
.
Co je sice pochopitelne, ale dost neprehladne - ktorekolvek zo standardnych znaceni je podla mna lepsie.
Oznacme si a
a

Vsimnime si, ze ak a
a  potom
potom 
a ze .
.
Ta prva vlastnost nie je moc podstatna pre to co pride, ale ta druha je.
Dalej mame

a teda


a to je ten tvar co si chcela.
Offline
#5 29. 01. 2014 12:21
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Konjugovaná funkce
↑ Brano:
Děkuji moc za vysvětlení. S tím značením máš pravdu. Nedokázala jsem předtím ty dvě podmínky dát do sebe, díky za dobrou vychytávku.
Jen jedna věc mi vrtá hlavou... vždy jsem si myslela, že platí ![kopírovat do textarea $\inf f(x) = \sup [- f(x)]$](/mathtex/bc/bc272d29576e00205e06d5e5389167a5.gif) , ale tys použil toto:
, ale tys použil toto: ![kopírovat do textarea $- \inf f(x) = \sup [- f(x)]$](/mathtex/b5/b55a5d65e06a219616900731a7bd4247.gif)
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#7 29. 01. 2014 16:11
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Konjugovaná funkce
↑ Brano:
Aha, děkuji moc.
Ještě mám k tomuto příkladu podúlohu a nejde mi se dopočítat konce.
Odvoďte tvar konjugované funkce: 
Zkoušela jsem ho odvodit z tvaru  , ale asi dělám něco špatně.
, ale asi dělám něco špatně.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#9 29. 01. 2014 17:52
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Konjugovaná funkce
↑ Brano:
Dělala jsem chybu v posledním výpočtu, kde se objevují dvě sumy, ale každá sumuje přes jiné indexy. Díky tvému indexu 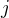 mi to došlo. Děkuji moc.
mi to došlo. Děkuji moc.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Konjugovaná funkce (TOTO TÉMA JE VYŘEŠENÉ)


 potom
potom  cize
cize  a
a  .
. pre
pre  a
a 
 s vazbou
s vazbou  teda
teda cize
cize , kde
, kde  z coho
z coho  teda
teda  .
. a teda
a teda co je to co si chcela.
co je to co si chcela.