Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 02. 2014 15:53
- karlherbert
- Příspěvky: 40
- Reputace: 0
Rovnice tečny ke grafu
Zdravím,
byl by mně někdo prosím ochotný pomoct s následujícím příkladem? Napište rovnici tečny ke grafu funkce y= 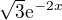 , která je rovnoběžná s přímkou y = -2x+3. Díky
, která je rovnoběžná s přímkou y = -2x+3. Díky
Offline
#2 02. 02. 2014 17:39 — Editoval Jj (02. 02. 2014 18:14)
#3 02. 02. 2014 17:53
- karlherbert
- Příspěvky: 40
- Reputace: 0
Re: Rovnice tečny ke grafu
↑ Jj: Děkji za odpověď ve výsledcích je: 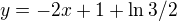 nějak nevím, jak se k tomu došlo, tedy resp, zda se používa pro tady tu transformaci vzorec:
nějak nevím, jak se k tomu došlo, tedy resp, zda se používa pro tady tu transformaci vzorec: nebo je to nějak jinak?
nebo je to nějak jinak?
Offline
#4 02. 02. 2014 17:58 — Editoval Jj (02. 02. 2014 18:13)
Re: Rovnice tečny ke grafu
↑ karlherbert:
Jé pardon - tam je chyba, hned se na to podívám!
Takže oprava od řádku: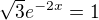
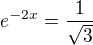
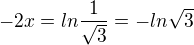
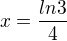
a tečna v tomto bodě vyjde podle výsledku: 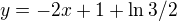
Pokud se tedy nemýlím.
Offline
#6 02. 02. 2014 18:22
Offline

