Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 05. 2012 16:09
- vasiksokol

- Příspěvky: 146
- Reputace: 0
logaritmy
potřeboval bych plsporadit 
Offline
- (téma jako vyřešené označil(a) vasiksokol)
#2 03. 05. 2012 16:12
Re: logaritmy
↑ vasiksokol:
stačí tak?
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#3 03. 05. 2012 16:12 — Editoval wolfito (03. 05. 2012 16:18)
Re: logaritmy
↑ vasiksokol:
Zdravím Tě,




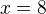
to byk7: nemuže to byt tak jak jsem to napsal ?
Radost z uvažování a z chápání je nejkrásnějším darem přírody.
Offline
#7 03. 05. 2012 16:19
Re: logaritmy
↑ wolfito:
Taky možnost... Ale autor nežádal celé řešení, chtěl jen poradit.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#14 04. 05. 2012 14:08
Re: logaritmy
↑ likeasir:
pro příště si založ vlastní téma
k dotazu: kdy je definován logaritmus?
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#16 04. 05. 2012 21:22 — Editoval byk7 (05. 05. 2012 13:48)
Re: logaritmy
↑ likeasir:
Pouze kladná čísla. Rovnost  totiž neplatí obecně, stačí porovnat definiční obory obou funkcí.
totiž neplatí obecně, stačí porovnat definiční obory obou funkcí.
Edit: kolega marnes to vysvětluje zde.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline




 nebo pouze kladná čísla?
nebo pouze kladná čísla?
