Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#58 10. 02. 2014 13:45
Re: Lineárna nerovnica
↑ crank139:
nulové body čitatel  , jmenovatel
, jmenovatel 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#59 10. 02. 2014 15:17 Příspěvek uživatele crank139 byl skryt uživatelem crank139. Důvod: ...
#61 10. 02. 2014 17:55
- janca361

- .
- Příspěvky: 3284
Re: Lineárna nerovnica
↑ crank139:


- Neprotne osu x.
Jedná se o kvadratickou nerovnici. Grafem kvadratické funkce je parabola. Na základě členu  je otočená nahoru a všechny hodnoty leží nad sou x. Žádné x menší než 0 neexistuje, proto je řešením prázdná množina.
je otočená nahoru a všechny hodnoty leží nad sou x. Žádné x menší než 0 neexistuje, proto je řešením prázdná množina.
Offline
#63 10. 02. 2014 18:36
- janca361

- .
- Příspěvky: 3284
Re: Lineárna nerovnica
↑ crank139:
Parabola opět neprotne osu x, podle  je celá na osou x. Ty hledáš všechna čísla větší nebo rovna 0. V tomto případně jsou to všechny čísla, tedy řešením je
je celá na osou x. Ty hledáš všechna čísla větší nebo rovna 0. V tomto případně jsou to všechny čísla, tedy řešením je  .
.
Offline
#65 10. 02. 2014 18:45
- janca361

- .
- Příspěvky: 3284
Re: Lineárna nerovnica
↑ crank139:
Musí tam být. Jak chceš řešit kvadratickou (ne)rovnici?
Offline
#67 10. 02. 2014 18:53
Re: Lineárna nerovnica
↑ crank139:
Dá se to řešit bez diskriminatu doplněním na čtverec


a součet dvou nezáporných čísel nemůže být záporný
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#68 10. 02. 2014 19:36 — Editoval crank139 (10. 02. 2014 19:48)
Re: Lineárna nerovnica

pri tomto príklade mi vyjde konečná nerovnica 
vo výsledkoch je že správna odpoveď je B no mne to vyšlo 
keď si totam dosadzujem tak mi vychádza že B by malo byť správne no neviem kde robím chybu že mi to v tabuľke vychádzá ako vychádza, a tu je spomínana tabuľka
ináč dasa rozložiť na štvorec aj  vďaka
vďaka
Offline
#69 10. 02. 2014 19:50
Re: Lineárna nerovnica
↑ crank139:
a mínus v čitateli ti to celé otočí
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#70 10. 02. 2014 19:57
Re: Lineárna nerovnica
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#72 10. 02. 2014 21:13
Re: Lineárna nerovnica
↑ crank139:
Můžeš, nemusíš.
Já osobně bych ještě tvou poslední nerovnici
upravil na
a pak je tvá tabulka bezproblémová
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

 či si sa len sekol? ináč to by bol prostredný interval aa ten mi hádže mínusove znamienko tak preto som ho tam nezaradil
či si sa len sekol? ináč to by bol prostredný interval aa ten mi hádže mínusove znamienko tak preto som ho tam nezaradil jsou přirozenými čísly čísla:
jsou přirozenými čísly čísla: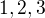 t jsou celkem tři čísla.
t jsou celkem tři čísla.

