Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 02. 2014 13:39 — Editoval Cheop (24. 02. 2014 14:35)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Offline
#3 24. 02. 2014 17:33 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#5 24. 02. 2014 22:16 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#7 25. 02. 2014 08:25 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: nonsense
#10 25. 02. 2014 14:17
#11 25. 02. 2014 15:09 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#12 25. 02. 2014 16:22 — Editoval vanok (25. 02. 2014 16:24)
Re: -
Poznamka:
Ina zabavna cesta k rieseniu: vynasobit vsetki tri rovnice, a z toho vyjadrit (r+1)(s+1)(t+1), a potom r,s,t.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#13 25. 02. 2014 19:21 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#14 25. 02. 2014 23:25 — Editoval vanok (26. 02. 2014 00:08)
Re: -
↑ paha154:,
Najprv predpokladaj, ze vsetki korene su kladne.
To da sucin (r+1)(s+1)(t+1)=24.
Del tuto rovnost prvou rovnicou, co da t+1=4, cize t=3. Atd....
Potom dokaz ze vsetky cleny sucinu su sucasne kladne alebo sucasne zaporne. A ine ich znamienka sa nemozu vyskytnut.
Tak a teraz uvazuj cely ten negativny pripad ... a dokonci.
Poznamka: treba pochopitelne presne vediet co je urcene a pytane kompletnym textom cvicenia
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#15 25. 02. 2014 23:31 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#16 25. 02. 2014 23:34
Re: -
Protože v původní soustavě máš součin dvou čísel vycházející kladně. A to platí pouze pro ++ nebo --. Kdyby ty znaménka byly namíchaný, tak by u jednoho vyšlo číslo záporné.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
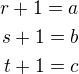 a pak už to nebude těžké.
a pak už to nebude těžké.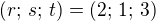
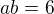
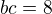
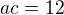
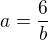
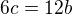 >>>
>>> 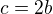
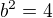 >>>
>>>