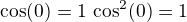Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita cos na cotg (TOTO TÉMA JE VYŘEŠENÉ)
#2 01. 02. 2009 23:09 — Editoval Marian (01. 02. 2009 23:09)
Re: Limita cos na cotg
↑ gekoncik:
Je
Protože funkce v základu i v exponentu jsou sudé, budeme moci vyšetřovat pouze jednu z jednostranných limit, třeba zprava. Využij toho, že platí (z definice obecné mocniny)  .
.
Offline
#4 01. 02. 2009 23:45
#6 02. 02. 2009 12:50 — Editoval Marian (02. 02. 2009 12:51)
Re: Limita cos na cotg
↑ gekoncik:Třetí řádek od konce dostaneš aplikací l'Hospitalova pravidla předchozího kroku. A k tomu, proč zmizel cos(x), resp. jeho druhá mocnina, je vysvětlení velmi snadné. Mohu totiž dosadit, protože cos(0)=1. Tím se výpočt zjednoduší. Doufám, že je jasný také zápis 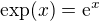 .
.
Offline
#8 02. 02. 2009 13:27 — Editoval Marian (02. 02. 2009 13:27)
#10 02. 02. 2009 13:39 — Editoval lukaszh (02. 02. 2009 13:43)
Re: Limita cos na cotg
↑ gekoncik:
Pretože ide o limitu súčinu dvoch funkcií, pričom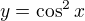
je spojitá v nule a nadobúda hodnotu 1, čiže:
Mohlo to byť urobené na základe predpokladu, že existujú vlastné limity oboch funkcií v súčine.
Ak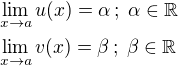
potom
Dôkaz si môžeš urobiť sám.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#11 02. 02. 2009 13:39
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita cos na cotg (TOTO TÉMA JE VYŘEŠENÉ)