Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 09. 2013 12:07
O grupe $S_3$
Co treba vediet o grupe 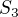 .
.
Urcite ( aj z dokazmy):
Rad prvkov grupy 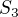 ,
,
Klasy konjugacii a centralisatory prvkov grupy 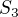 .
.
Podgrupy grupy 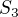 ako aj
ako aj
jej normalne podgrupy a korespodujuce grupy quotient (groupe quotient).
Tiez klasy konjugacii a normalizatory podgrup grupy 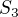 .
.
Centrum 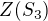 grupy
grupy 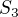 .
.
Tiez aj jej grupu komutatorov &D(S_3)$ (groupe dérivé).
Na osviezenie pojmov:
http://en.wikipedia.org/wiki/Conjugacy_class
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 24. 09. 2013 23:52
Re: O grupe $S_3$
Ahoj ↑ Andrejka3:
napriklad takto:
Id,(1,2),(1,3),(2,3),(1,2,3),(1,3,2)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 25. 09. 2013 08:38 — Editoval Andrejka3 (29. 09. 2013 13:01)
Re: O grupe $S_3$
Ostatní později.
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 25. 09. 2013 12:11
Re: O grupe $S_3$
Ahoj ↑ Andrejka3:,
Si na dobrej ceste.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 25. 09. 2013 12:22
Re: O grupe $S_3$
Ahoj ↑ Brano:,
To je pravda, ale asi kazdy student by to mal aspon raz pocitivo urobit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 29. 09. 2013 12:48 — Editoval Andrejka3 (29. 09. 2013 13:02)
Re: O grupe $S_3$
Zbývají
vanok napsal(a):
...normalizatory podgrup grupy
.
Tiez aj jej grupu komutatorov &D(S_3)$ (groupe dérivé).
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 29. 09. 2013 14:44 — Editoval vanok (02. 10. 2013 00:10)
Re: O grupe $S_3$
Ahoj ↑ Andrejka3:,
Poznamka:
na tuto otazku staci pouzit znamu definiciu:
Centralisator prvku x grupy G, je mnozina vsetkych jej prvkov co komutuju z x.
V tomto cviceni pre kazdy prvok 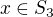 je jeho centralisator grupa ktoru generuje:
je jeho centralisator grupa ktoru generuje:  az pre
az pre 
Dobre dokoncenie.
Edit: oprava preklepu opravena, vdaka tvojej poznamke.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 29. 09. 2013 15:27
Re: O grupe $S_3$
Ano az na identitu. Prave som to isiel opravit.
To je dobra reakcia, co ukazuje ze pozorne citas odpovede.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 01. 10. 2013 21:31
Re: O grupe $S_3$
↑ Andrejka3:
Normalizátory podgrup
What does a drowning number theorist say?
'log log log log ...'
Offline
#13 02. 10. 2013 13:04
Re: O grupe $S_3$
Ahoj ↑ Andrejka3:,
Toto moze byt uzitocne.
Troska teorie
Vieme ze 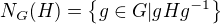 definuje stabilizator podgrupy
definuje stabilizator podgrupy  v
v 
Potom mozme definovat normalizator podgrupy  c
c  ako
ako 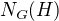 taku ze
taku ze  a
a 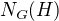 najvadcia podgrupa grupy
najvadcia podgrupa grupy  co ma tuto vlasnost.
co ma tuto vlasnost.
Priklad: Podgrupa 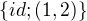 grupy
grupy 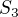 je jej vlastny normalizator.
je jej vlastny normalizator.
Pozri aj toto:
http://en.wikipedia.org/wiki/Normalizer
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 02. 10. 2013 13:19
Re: O grupe $S_3$
Přijde mi legrační, že anglická a francouzská wiki mají 'inverzne' definovany komutator. Zajimalo by me, jestli ke kazde konvenci existuje svuj duvod, nebo je to uplne jedno.
What does a drowning number theorist say?
'log log log log ...'
Offline
#15 02. 10. 2013 13:55
Re: O grupe $S_3$
↑ Andrejka3:
To je eqvivalentne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 02. 10. 2013 14:16 — Editoval Andrejka3 (02. 10. 2013 20:26)
Re: O grupe $S_3$
Podgrupa derivaci.
Jo, ekvivalentni to je. Vsimla jsem si ale treba, ze kdybychom definovali vnitrni automorfismus urceny prvkem g inverzne, není pak prirazeni
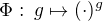 , kde
, kde 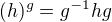 homomorfismem (je antihomomorfismem)? Tak jsem si říkala, jestli tam nebude taky něco podobného.
homomorfismem (je antihomomorfismem)? Tak jsem si říkala, jestli tam nebude taky něco podobného. What does a drowning number theorist say?
'log log log log ...'
Offline
#17 02. 03. 2014 11:49 — Editoval Andrejka3 (02. 03. 2014 13:49)
Re: O grupe $S_3$
Grupa derivací  .
.
edit přidám další postupně pro S_n.
Klasy konjugací
To není ze skript, psala jsem to, takže tam mohou být chyby.
Centrum
Řády prvků
Nevím ale, co napsat o podgrupách, normálních podgrupách a normalizers. Snad až na použití Sylow vět -- že existují nějaké p-grupy a jakého řádu jsou atd.?
What does a drowning number theorist say?
'log log log log ...'
Offline

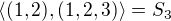 , menší množina generátorů neexistuje.
, menší množina generátorů neexistuje. .
.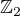 .
.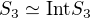 (snad to je pravda).
(snad to je pravda).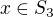 platí
platí 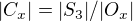 , kde C_x je stabilizátor prvku x, a zde v případě akce dané přiřazením příslušného vnitřního automorfismu je to i centralisator, O_x je orbita příslušná x. Odtud
, kde C_x je stabilizátor prvku x, a zde v případě akce dané přiřazením příslušného vnitřního automorfismu je to i centralisator, O_x je orbita příslušná x. Odtud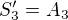 nebo
nebo  . Každý komutátor je ale permutací sudou, takže pravdivá je ta první možnost, tj.
. Každý komutátor je ale permutací sudou, takže pravdivá je ta první možnost, tj. 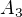 .
. .
.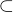 :'
:' ![kopírovat do textarea $\mathrm{sgn}\hspace{1pt}[g,h]=ghg^{-1}h^{-1}=(\mathrm{sgn}\hspace*{1pt}g)^2\cdot(\mathrm{sgn}\hspace*{1pt}h)^2=1$](/mathtex/32/32c5898acbc293e6d9cf415eebd4cc23.gif) .
. ':
': 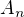 je generována
je generována  -cykly. Každý trojcyklus je komutátorem dvou transpozic:
-cykly. Každý trojcyklus je komutátorem dvou transpozic:![kopírovat do textarea $\begin{pmatrix}1&2&3 \end{pmatrix}=[(12),(13) ]=[(12)(13)]^2=(132)^2=(123)$](/mathtex/6d/6d5d4ec7e99b6e0e7496e7040990010c.gif) .
.


 , kde
, kde  je počet i-prvkových orbit permutace.
je počet i-prvkových orbit permutace.

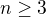 .
. . Komutuje tedy s každou transpozicí.
. Komutuje tedy s každou transpozicí.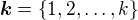 ,
,  .
.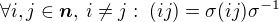 . Pak ale
. Pak ale 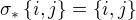 díky tvrzení o prvcích, které konjugují dvě permutace (viz klasy konjugací). Kdybychom připustili
díky tvrzení o prvcích, které konjugují dvě permutace (viz klasy konjugací). Kdybychom připustili 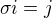 pak pro nějaké
pak pro nějaké 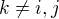 (takové existuje, protože n>2) je
(takové existuje, protože n>2) je 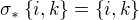 a na druhou stranu
a na druhou stranu 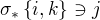 . To je spor. Odtud,
. To je spor. Odtud, 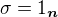 .
.