Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 03. 03. 2014 20:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: -
Zdravím,
Toto je prý příklad pro žáka základní školy a já si s tím lámu hlavu už od rána.
to není div - mají jiný pohled na svět.
Můj návrh - začnu s trojúhelníkem na 3 různých vrcholech (neleží na jedné přímce a mají různé barvy dle zadání. Dovnitř trojúhelníku umístím bod libovolné barvy, opět mohu vytvořit trojúhelník splňující požadavek atd.
Předpokládám, že někdo z kolegů bude mít více použitelné řešení.
Offline
#3 04. 03. 2014 12:07
Re: -
↑ paha154:, ↑ jelena:
Zdravím .
Aby věta platila, přidejme jednoduchý předpoklad, že z daných bodů žádné tři neleží v jedné přímce (asi by se dal zeslabit,
ale to teď neřešme).
Zkusím rozvést myšlenku od kolegyně Jeleny do formálního důkazu.
Nechť 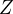 je množina bodů splňujících předpoklady věty.
je množina bodů splňujících předpoklady věty.
Budeme říkat, že bod  patří trojúhelníku
patří trojúhelníku  , je-li jeho vrcholem či vnitřním bodem.
, je-li jeho vrcholem či vnitřním bodem.
O trojúhelníku s vrcholy v množině 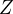 budeme říkat, že je trojbarevný, právě když každý jeho vrchol je obarven jinou barvou.
budeme říkat, že je trojbarevný, právě když každý jeho vrchol je obarven jinou barvou.
Označme  množinu všech trojbarevných trojúhelníků. Z předpokladů věty plyne, že
množinu všech trojbarevných trojúhelníků. Z předpokladů věty plyne, že  .
.
Je-li 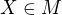 , pak nechť
, pak nechť 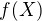 je počet těch bodů množiny
je počet těch bodů množiny 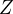 , které patří trojúhelníku
, které patří trojúhelníku  , takže vždy je
, takže vždy je 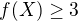 .
.
Máme dokázat, že existuje trojúhelník  takový, že
takový, že 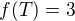 (což by znamenalo, že žádný bod množiny
(což by znamenalo, že žádný bod množiny 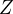
není jeho vnitřním bodem).
Množina
(0) 
je neprázdnou částí množiny všech přirozených čísel a má tedy svůj nejmenší prvek  .
.
Jde o to dokázat, že 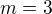 - odtud vyplyne existence trojúhelníka
- odtud vyplyne existence trojúhelníka  s vlastností
s vlastností 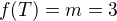 . Dokazujme sporem.
. Dokazujme sporem.
Předpokládejme, že  a
a  s vrcholy
s vrcholy 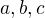 je takový, že
je takový, že 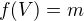 . To znamená, že uvnitř trojúhelníka
. To znamená, že uvnitř trojúhelníka 
existuje 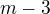 bodů množiny
bodů množiny 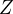 , které jsou samozřejmě různy od bodů
, které jsou samozřejmě různy od bodů 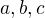 . Je-li
. Je-li  jedním z těchto
jedním z těchto  bodů, pak je
bodů, pak je
barevně shodný s právě jedním z bodů 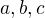 - bez újmy na obecnosti předpokládejme, že s bodem
- bez újmy na obecnosti předpokládejme, že s bodem  . Snadno lze nahlédout,
. Snadno lze nahlédout,
že o trojúhelníku  s vrcholy
s vrcholy 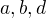 platí následující dvě tvrzení:
platí následující dvě tvrzení:
(1)  je trojbarevný (tedy
je trojbarevný (tedy 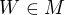 ) ,
) ,
(2) každý bod patřící trojúhelníku  patří též trojúhelníku
patří též trojúhelníku  .
.
Odtud vyplývá  . Avšak rovněž je zřejmé, že bod
. Avšak rovněž je zřejmé, že bod  (partřící trojúhelníku
(partřící trojúhelníku  ) nepatří trojúhelníku
) nepatří trojúhelníku  ,
,
proto  , takže také
, takže také  . To je ale ve sporu s volbou čísla
. To je ale ve sporu s volbou čísla  jakožto nejmenšího prvku množiny
jakožto nejmenšího prvku množiny  z (0).
z (0).
Offline
#4 04. 03. 2014 13:45 — Editoval vanok (04. 03. 2014 14:12)
Re: -
Pozdravujem,
Intuitivny neformalny dokaz.
Treba pochopitelne predpokladat, ze aspon jeden trojfarebny trojuholnik
existuje. (pod pojmom trojfarebny trojuholnik, rozumiem taky ktoreho vrcholy su roznej farby aj z jeho obvodom)
Ak mame jeden trojfarebny trojuholnik, co obsahuje farebne body, tak vyber z jedneho z nich, dovoluje vytvorit novy 3jfarebny trojuholnik, ktory obsahuje menej farebnych bodov ako predosly.
Cize po konecnom poctu krokov dostaneme jeden trojfarebny trojuholnik co vyhovuje problemu.
Poznamka:
I ked taketo riesenie malo ziakov najde, ale asi skoro vsetci ho mozu pochopit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 04. 03. 2014 14:49 — Editoval paha154 (04. 03. 2014 14:53)
Re: -
↑ jelena:, ↑ vanok::
To jsou velice hezké a pochopitelné důkazy, takhle mě nenapadlo se na to dívat. Díky!
↑ Rumburak::
Díky za tento důkaz. Sice si ho ještě musím párkrát přečíst a popřemýšlet, než mi to bude zcela jasné, ale jinak je srozumitelný.
Offline
#6 06. 03. 2014 19:21 — Editoval paha154 (06. 03. 2014 20:14)
Re: -
Ještě bych potřeboval trochu nakopnout, nedochází mi totiž ten závěr toho důkazu...
Jak to, že je to v rozporu?
My předpokládali, že m>3 a vyšlo nám, že f(W)<m, to ale znamená, že můžu najít ještě trojúhelník, který je "podmnožinou" toho trojúhelníku W, ne? Protože my to m=3 měli ještě před tím sporem a pak jsme předpokládali právě, že m>3 a to se nám neodporovalo, ne? Nebo jo a já to v tom prostě nevidím???
Zkrátka tyto dva řádky:
Odtud vyplývá
. Avšak rovněž je zřejmé, že bod
(partřící trojúhelníku
) nepatří trojúhelníku
,
proto, takže také
. To je ale ve sporu s volbou čísla
jakožto nejmenšího prvku množiny
z (0).
nemůžu pochopit. :-(
Offline
#7 06. 03. 2014 21:41 — Editoval check_drummer (06. 03. 2014 21:43)
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: -
Ahoj,
vyhovme ještě kolegovi a nastiňme požadované řešení, která má využívat "maxima nebo minima": Zvolme ze všech trojúhelníků, jehož 3 vrcholy jsou obarveny různou barvou takový, který má minimální obsah. Pak je on tím hledaným trojúhelníkem. (Důkaz je podobný jako důkazy výše, dokážeme sporem.)
Edit: Vidím, že kolega Rumburak myšlenku minima použil (avšak automatické vyhledání selhalo, protože šlo o nejmenší prvek).
"Máte úhel beta." "No to nemám."
Online
#8 07. 03. 2014 09:33 — Editoval Rumburak (07. 03. 2014 10:05)
Re: -
↑ paha154:
Číslo  bylo zavedeno jako nejmenší prvek množiny
bylo zavedeno jako nejmenší prvek množiny  (na základě věty, že každá neprázdná část množiny přirozených čísel
(na základě věty, že každá neprázdná část množiny přirozených čísel
obsahuje svůj nejmenší prvek, při čemž  je takovou částí). Výsledek
je takovou částí). Výsledek  odvozený z předpokladu
odvozený z předpokladu
(P) 
však říká, že v množině  byl nalezen prvek menší než
byl nalezen prvek menší než  , a sice prvek
, a sice prvek 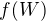 (jelikož o nalezeném trojúhelníku
(jelikož o nalezeném trojúhelníku  platí
platí 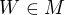 ) . Pak by ale číslo
) . Pak by ale číslo  nemohlo být nejmenším prvkem množiny
nemohlo být nejmenším prvkem množiny  . To je ten spor. Vedl k němu předpoklad (P),
. To je ten spor. Vedl k němu předpoklad (P),
takže tento předpoklad musí být nesprávný, protože ze správných předpokladů by spor nemohl vyplynout.
Offline
