Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 03. 2014 21:44
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Geometricka posloupnost, rovnice
Zdravim,
mel bych tu jeden priklad, se kterym si nevim rady![kopírovat do textarea $x\sqrt{x^3}*\sqrt[4]{x^3}*\sqrt[8]{x^3}=16$](/mathtex/a2/a238fe02ff1679818e0a6e0d469a6d42.gif)
Neporadim si s prvnim clenem a kvocientem.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 07. 03. 2014 21:57
Re: Geometricka posloupnost, rovnice
↑ cutrongxoay:↑ cutrongxoay:
co mas vypocitat x? nemas vysledok?
Offline
#3 08. 03. 2014 09:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometricka posloupnost, rovnice
↑ cutrongxoay:
Zdravím,
přímo v tomto zápisu nutnost geometrické posloupnosti nevidím - pokud je to originál zadání, výraz nalevo můžeš upravit do tvaru x^(...)=16 a dořešit vzniklou rovnici - je tak? Děkuji.
Offline
#4 08. 03. 2014 11:48
#5 08. 03. 2014 11:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometricka posloupnost, rovnice
↑ cutrongxoay:
podle mne vychází tak, že zadání odpovídá (na tom bych nic divného neviděla, případně udělej zkoušku). Je možné, že v úloze je nějaký překlep. Pokud by byla úloha na použití vzorce pro nekonečnou geom. řadu, potom by bylo v zadání alespoň ... na konci levé strany a součty, ne násobení. Zkusím kouknout do sbírek, zda něco podobného nenajdu.
Offline
#6 08. 03. 2014 11:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometricka posloupnost, rovnice
↑ cutrongxoay:
v "Sbírka maturitních příkladů" je "stanovte součin ![kopírovat do textarea $x\cdot \sqrt{x^3}\cdot \sqrt[4]{x^3}\cdot\sqrt[8]{x^3}\cdot \sqrt[16]{x^3}\cdot \ldots$](/mathtex/47/47cc66abfd6a3d85ddc5fa6eab114499.gif) bz mohlo být nejblíž Tvému zadání.
bz mohlo být nejblíž Tvému zadání.
Offline
#7 08. 03. 2014 12:07
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Geometricka posloupnost, rovnice
↑ jelena:
Asi to tomu odpovida.
Dekuji moc, jsme zatim u souctu, o soucinu jeste nemam poneti.
Offline
#8 08. 03. 2014 12:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometricka posloupnost, rovnice
↑ cutrongxoay:
zkus pouvažovat nad využitím nekon. geom. řady v součtů exponentů (při úpravě dle pravidel mocnin).
Offline
#9 08. 03. 2014 12:16
Re: Geometricka posloupnost, rovnice
Tváří se to jako součin, ale je to ve skutečnosti součet, protože když násobíš mocniny o stejném základu, tak sčítáš jejich exponenty. Zde stačí spočítat součet exponentů: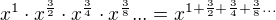
Součet: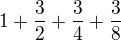 zvládneš? je to vlastně:
zvládneš? je to vlastně: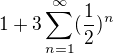
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#10 08. 03. 2014 12:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometricka posloupnost, rovnice
↑ Freedy:
Zdravím,
funguje Tobě tlačítko Náhled? Proč nenecháš kolegu chvilku pouvažovat nad návrhem v mém příspěvku č.8? Hoří snad někde? Děkuji.
Offline
#11 08. 03. 2014 12:29 — Editoval cutrongxoay (08. 03. 2014 12:41)
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Geometricka posloupnost, rovnice
↑ jelena:
Jsem si take vedom toho, ze se exponenty scitaji.
Ja spis nerozeznam prvni clen a kvocient teto rady, abych mohl urcit soucet a dat ho do rovnosti s pravou stranou.
/edit
Jestli je rada takova ,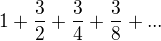
mam brat 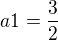 a
a  ?
?
pak 
====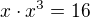

Je to tak?
Offline
#12 08. 03. 2014 12:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometricka posloupnost, rovnice
↑ cutrongxoay:
pokud tedy pracujeme s upraveným zadáním rovnice:![kopírovat do textarea $x\cdot \sqrt{x^3}\cdot \sqrt[4]{x^3}\cdot\sqrt[8]{x^3}\cdot \sqrt[16]{x^3}\cdot \ldots=16$](/mathtex/d8/d80bed0f74d53bbcbe3a046a95c1ec28.gif)
tak řada je jen v součtu exponentů, tedy na x chvilku zapomeň, sestav výsledek součtu pro exponent (s použitím vzorce pro nekon. řadu) a potom dokončíš celou rovnici. Řadu v součtu exponentů vidíš a najdeš 1. člen a q?
Offline
#13 08. 03. 2014 13:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometricka posloupnost, rovnice
↑ cutrongxoay:
děkuji za edit, také mi tak vyšlo.
Offline
#14 08. 03. 2014 14:02
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Geometricka posloupnost, rovnice
Dekuji za pomoc
Offline
#15 08. 03. 2014 15:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometricka posloupnost, rovnice
↑ cutrongxoay:
není za co, označím za vyřešené.
Offline

