Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 03. 2014 17:10
Kružnice a přímka
Ahoj, moc prosím o pomoc s příkladem ze Sbírky úloh pro gymnázia (Analytická geometrie).
Vypočítejte velikost úhlu, po kterým je vidět kružnice k z bodu R. k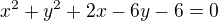 : ;
: ; ![kopírovat do textarea $R [3,0]$](/mathtex/06/0620eda19fe4c0ba9eaf032eaa6d56b5.gif) .
.
Příklad jsem počítala už 2x, ale stále se nemůžu dobrat správného výsledku. Stačily by mi pouze souřadnice tečen, které mi vycházejí stále špatně.
Díky moc za pomoc
Offline
#2 08. 03. 2014 17:12
- janca361

- .
- Příspěvky: 3284
Re: Kružnice a přímka
↑ Sheldon.C:
Ahoj, napiš jak počítáš a co ti vychází.
Díky.
Offline
#3 08. 03. 2014 18:29
Re: Kružnice a přímka
Vyjádřila jsem si, že  a dosadila do rovnice, poté mi vyšlo, že D=5184 =>
a dosadila do rovnice, poté mi vyšlo, že D=5184 => 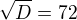 . Body mi vyšly:
. Body mi vyšly: ![kopírovat do textarea $T1=[3,3]$](/mathtex/79/7913bed3f6c6f8d6943b399651cc4ad8.gif) a
a ![kopírovat do textarea $T2=[\frac{3}{25},-\frac{21}{25}]$](/mathtex/39/3951d7309d9b9e56a7d0b980718c9b26.gif) , udělala jsem rovnice tečen a potom si vytáhla normálové vektory rovnic tečen. Ale úhel mi už potřetí vyšel okolo
, udělala jsem rovnice tečen a potom si vytáhla normálové vektory rovnic tečen. Ale úhel mi už potřetí vyšel okolo 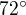 a ve výsledcích je
a ve výsledcích je 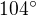 . Vůbec nevím, kde dělám dokola pořád tu stejnou chybu. Děkuji
. Vůbec nevím, kde dělám dokola pořád tu stejnou chybu. Děkuji
Offline
#5 08. 03. 2014 21:57
Re: Kružnice a přímka
↑ Sheldon.C:
Dobrý večer.
Body dotyku jsou podle mě v pořádku. Řekl bych, že asi počítáte omylem doplňkový úhel (doplněk do 180°).
Pokud se tedy nemýlím.
Offline
#9 09. 03. 2014 13:05 — Editoval Jj (09. 03. 2014 13:09)
Re: Kružnice a přímka
↑ Sheldon.C:
Řekl bych, že je to normální, záleží na orientaci vektorů, který úhel 'vyjde':
kosinus úhlu vektorů (7,-24) a (1,0) bude 
kosinus úhlu vektorů (-7, 24) a (1,0) bude 
Oba první vektory jsou přitom směrovými vektory tečny 7 x-24 y-21 = 0.
Bývá dobré udělat si náčrtek.
Poznámka: Pro úhel přímek nemusíte "vytahovat" normálové vektory, mají stejný úhel jako jejich směrové vektory (úhly, jejichž ramena jsou na sebe kolmá, jsou shodné).
Edit - doplněno: Odpověď jsem tvořil, když jsem neviděl předcházející příspěvek. Takže jsou některé části "dublované". Už to nebudu upravovat.
Pokud se tedy nemýlím.
Offline
#11 09. 03. 2014 14:28
Re: Kružnice a přímka
↑ Sheldon.C:
Vzoreček pro úhel dvou přímek je sestaven tak, aby obecně dával jejich ostrý úhel. Pokud Vás zajímá jejich tupý úhel (jako u této konkrétní úlohy), provedete dopočet do 180°.
Nebo můžete využít toho, že pro úhel dvou vektorů (jakoby šipek vycházejících z téhož bodu) toto omezení není až tak účelné. Proto se počítá bez absolutní hodnoty a úhly se uvažují v rozmení 0° - 180° (striktně vzato záporný kosinus je i pro úhly ve III. kvadrantu - pak byste obdržela i jejich vypuklý úhel).
Pokud se tedy nemýlím.
Offline
#13 10. 03. 2014 08:08
Re: Kružnice a přímka
↑ Sheldon.C:
Podle toho zda je skalární součin směrových (nebo normálových) vektorů přímek kladný nebo záporný (tj. jaké je znaménko u kosinu).
Ten vzoreček pro úhel dvou přímek (s absolutní hodnotou) totiž vždy dává úhel v rozmezí 0-90 st.
V úloze máš ale vypočítat úhel, pod kterým je vidět elipsa a ten může být samozřejmě i větší než 90 st.
Offline
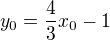

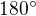 vyšel správný výsledek. Vůbec ale nevím, proč se to má odečítat? V předchozích příkladech jsme to nikde nedělali.
vyšel správný výsledek. Vůbec ale nevím, proč se to má odečítat? V předchozích příkladech jsme to nikde nedělali.![kopírovat do textarea $t_{1} v T_{1}[3,3]: x-3=0$](/mathtex/19/1981e84637fc4569daabc601db8030e9.gif)
![kopírovat do textarea $t_{2} v T_{2}[\frac{3}{25},-\frac{21}{25}]: 7x-24y-21=0$](/mathtex/a3/a30a0c79ace58fbceab2a5fa5dbc6615.gif)
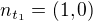 a
a