Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 03. 2014 21:33
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Nekonečná geom. řada
Zdravím,
rád bych zeptal na tento příklad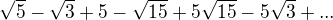
Nenacházím v tom žádný systém, je to možné?
Offline
- (téma jako vyřešené označil(a) cutrongxoay)
#2 11. 03. 2014 21:37 — Editoval gadgetka (11. 03. 2014 21:47)
Re: Nekonečná geom. řada
Ahoj, stačí výraz trochu upravit, abys dostal kvocient: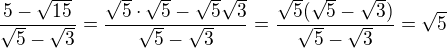
Edit: Druhý kvocient ale nevychází stejný... ještě na to mrknu
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 11. 03. 2014 22:23 — Editoval cutrongxoay (11. 03. 2014 22:28)
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Nekonečná geom. řada
↑ gadgetka:
Dekuji, je to mozne, zadani mame vytistene, takze za spravnost nemohu rucit.
Navic me nenapadlo brat 2 cleny, celou dobu jsem bral jen jeden clen, tim padem vychazel kvocient mezi kazdym clenem jinak
Edit:
Takze jestli dobre chapu, nemusim brat pomer mezi jednotlivym clenem, ale i mezi dvema, tremi, ... cleny. Je to tak?
Offline
#6 11. 03. 2014 22:29
Re: Nekonečná geom. řada
Pokud by to bylo bez překlepu, tak stačilo zkontrolovat členy ob jeden, a též je kvocientem  , jen bys tu řadu rozdělil na dvě.
, jen bys tu řadu rozdělil na dvě.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline

 , pak by
, pak by 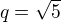 , nemáš špatně opsaný příklad?
, nemáš špatně opsaný příklad?
 pak bereš celý ten člen
pak bereš celý ten člen