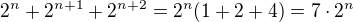Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 03. 2014 06:14
- lukasstork

- Příspěvky: 57
- Reputace: 0
Dukazy
Ahoj potreboval bych pomoc s dukazy těchto tři vět, jestli byste mi mohli pomoct
V1: Součet dvou dvojciferných čísel, která se liší pouze pořadím cifer, je dělitelný 11. V2: Rozdíl dvou dvojciferných čísel, která se liší pouze pořadím cifer, je dělitelný 9. V3:Součet tří mocnin čísla 2, kde exponenty jsou čísla po sobě jdoucí, je dělitelný 7.
Offline
- (téma jako vyřešené označil(a) gadgetka)
#2 15. 03. 2014 10:04
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Dukazy
↑ lukasstork: Ahoj,
k prvým dvom vetám: skús si pôvodné dvojciferné číslo napísať v tvare 10A+B (A, B sú cifry), keď cifry prehodíme, dostaneme 10B+A. Tieto dve čísla sčítaj a odčítaj, potom by to už malo byť vidno.
Offline
#3 15. 03. 2014 10:14
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: Dukazy
Takze na konci mam vytknout 11 jestli to dobre chapu u ty 1. Vety
Offline