Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » poloměr konvergence (TOTO TÉMA JE VYŘEŠENÉ)
#2 03. 02. 2009 22:58
Re: poloměr konvergence
↑ veronica:
Myslím, že to je správne.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 04. 02. 2009 12:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: poloměr konvergence
↑ veronica:
Není mi jasné  . r má být poloměr konvergence? Pak je ale přece
. r má být poloměr konvergence? Pak je ale přece 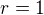 .
.
Součet není dobře, asi jsi zapomněla na to, že první člen řady  je x, ne 1. Součet je tedy
je x, ne 1. Součet je tedy .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » poloměr konvergence (TOTO TÉMA JE VYŘEŠENÉ)
 a pomocí vhodné úpravy (derivování resp. integrování člen po členu) určete její součet.
a pomocí vhodné úpravy (derivování resp. integrování člen po členu) určete její součet.
