Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 03. 2014 21:28
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
expo/iracionální rovnice
Ahoj, potřeboval bych pomoc s příkladem. 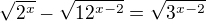 Nevím, zda začít jako s iracionální či exponenciální rovnicí, či je to jedno? Každopádně se nemůžu dostat k výsledku. Který je 2 mimochodem.
Nevím, zda začít jako s iracionální či exponenciální rovnicí, či je to jedno? Každopádně se nemůžu dostat k výsledku. Který je 2 mimochodem.
Byl bych rád za nakopnutí. A radu co obecně dělat, když mám u exponenciálních rovnic na jedné straně součin dvou různých základů.
Děkuji :)
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#2 19. 03. 2014 21:32
- janca361

- .
- Příspěvky: 3284
Re: expo/iracionální rovnice
↑ jelinekgreen:
Prvně bych se u takových příkladů dívala, zda není možné provést substituci - tady nic vhodného není.
Tahže zbavit odmocnin, tj. umocnit "na druhou" - budou nějaké podmínky?
A potom vznikne exponenciální rovnice a tu řešit.
Offline
#3 19. 03. 2014 21:53
#4 19. 03. 2014 22:07
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: expo/iracionální rovnice
Já už to zkoušel tak i tak a nic.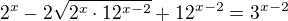
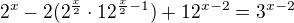
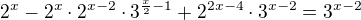
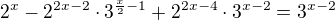
A dál nevím.
Na tomhle příkladu fakt krvácím
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#6 19. 03. 2014 23:00
Re: expo/iracionální rovnice
Všeobecná rada, ako takéto úlohy riešiť.
Pri tejto bolo dobré použiť nerovnosti resp. úvahy o funkciách a uhádnutie riešenia.
(ako tu: http://forum.matweb.cz/viewtopic.php?id=68305)
Typicky sa však v tých stredoškolských úlohach používa substitúcia po vhodnom vydelení.
Napríklad:
Upravíme na 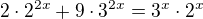
Vydelíme 
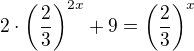
...
1^6 - 2^6 + 3^6 = 666
Offline
#7 20. 03. 2014 10:49
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: expo/iracionální rovnice
↑ BakyX: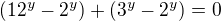
Vůbec nerozumím úpravě na druhém řádku. 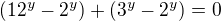 Jak se na tohle dostanu??
Jak se na tohle dostanu??
A po tomto 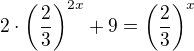 pokračuju jak? Úplně jsem se ztratil...
pokračuju jak? Úplně jsem se ztratil...
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#8 20. 03. 2014 10:53
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: expo/iracionální rovnice
↑ BakyX:
Já jsem se při jednom z pokusů dostal při substituci 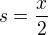 na tvar:
na tvar: 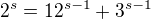 , což by mělo vyjít. Ale nevím, jak z toho tvaru dál. Uniká mi nějaký zásadní způsob řešení :D Pomoc prosím..
, což by mělo vyjít. Ale nevím, jak z toho tvaru dál. Uniká mi nějaký zásadní způsob řešení :D Pomoc prosím..
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#10 20. 03. 2014 11:19 — Editoval Rumburak (20. 03. 2014 11:53)
Re: expo/iracionální rovnice
↑ jelinekgreen:
Ahoj.
Kolega ↑ BakyX: možná postupuje na Tebe příliš rychle. Moje doporučení:
Vrať se k původní rovnici
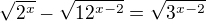
a začni tím, že se zbavíš druhé odmocniny jejím převodem na racionální exponent podle vzorce  .
.
Dostaneš (po mírné úpravě)
Nyní by se hodilo provést (první) substituci
 EDIT nebo ještě lépe
EDIT nebo ještě lépe 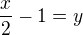 .
. V dalším postupu se využije faktu, že
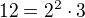 .
. Offline
#11 20. 03. 2014 11:19
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: expo/iracionální rovnice
↑ byk7:
Dobře, tohle jsem pochopil. Můžu se ale dobrat výsledku nějakým uceleným způsobem a ne úvahou nad rovnostma?
Když mám tedy na pohled celkem jednoduchou rovnici 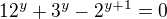 , jak vyjádřím y??
, jak vyjádřím y??
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#12 20. 03. 2014 11:48 — Editoval Rumburak (20. 03. 2014 11:56)
Re: expo/iracionální rovnice
↑ jelinekgreen:
Rovnici 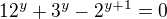 vydělíme nenulovým výrazem
vydělíme nenulovým výrazem 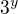 . Odtud
. Odtud
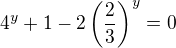 ,
,
 .
.
Funkce tvořící levou stranu poslední rovnice je rostoucí (základ exp. fce je > 1) a zobrazuje  na
na  ,
,
funkce tvořící pravou stranu téže rovnice je klesající (základ exp. fce je < 1) a zobrazuje  na
na  ,
,
při čemž obě tyto funkce jsou spojité.
Odtud plyne (pro orientaci pomůže náčrtek), že tato rovnice má řěšení, a sice právě jedno. Zkusmo zjistíme, že  .
.
Offline
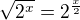 , není třeba nic umocňovat.
, není třeba nic umocňovat.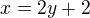 . Dostávame rovnicu
. Dostávame rovnicu je
je  a
a  , žiadne riešenie.
, žiadne riešenie. naopak
naopak  a
a  , žiadne riešenie.
, žiadne riešenie. , čo je riešením.
, čo je riešením.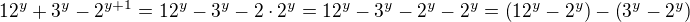
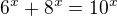
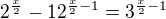 ,
,