Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 03. 2014 14:21
Hyperbola
Ahoj, moc prosím o radu s příkladem:
Určete velikost úhlu, pod kterým je z bodu ![kopírovat do textarea $H[-12,2]$](/mathtex/df/df7de49bb308dc9077ff4207b2a6808d.gif) vidět hyperbolu o rovnici
vidět hyperbolu o rovnici
Našla jsem zde řešený stejný příklad z roku 2011, ale nebyl nijak vyřešen. Já jsem postupovala trošku jinak.
1. ![kopírovat do textarea $t v T[x_{0},y_{0}]: 4(x-3)\cdot (x_{0}-3)-45(y+2)\cdot (y_{0}+2)=180$](/mathtex/ad/adcf3bfd2723ba217ca7f8ebb0eda34f.gif)
2.  :
: 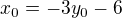
3. 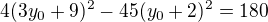
po úpravě: 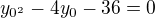
D=160
Zaráží mě výsledek diskriminantu 160, z čehož potom vyjde, že 
Je to dobře? Případně jak mám teď vypočítat úhel?
Děkuji moc
Offline
#2 29. 03. 2014 14:55
Re: Hyperbola
↑ Sheldon.C:
Dobrý den, není nějaká chyba v zadání? Bod ![kopírovat do textarea $H[-12,2]$](/mathtex/df/df7de49bb308dc9077ff4207b2a6808d.gif) je (pokud jsem se nepřepočítal) bodem hyperboly
je (pokud jsem se nepřepočítal) bodem hyperboly  . Má se počítat, jak je hyperbola vidět ze "svého" bodu?
. Má se počítat, jak je hyperbola vidět ze "svého" bodu?
Pokud se tedy nemýlím.
Offline
#4 29. 03. 2014 15:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Hyperbola
Zdravím,
↑ Sheldon.C: to je téma, co jsi našla. Pokud je bod H na hyperbole, potom nevidíme tu větev hyperboly, na které bod leží, ale druhou větev, pro kterou tento bod bude vnějším bodem pro tečny (a jejich odchylku hledáme). Tak jsem si úlohu představovala v odkazovaném tématu. Souhlasí to? Děkuji.
Offline
#6 29. 03. 2014 18:54 — Editoval Jj (29. 03. 2014 18:54)
Re: Hyperbola
↑ jelena: ↑ Sheldon.C:
Zdravím. Nějak se neumím srovnat s tím, že z bodu jedné větve hyberboly má jít spouštět tečny na její druhou větev. To je podle mně "proti přírodě":
Řekl bych podle obrázku, že zorný úhel, pod nímž je vidět druhou větev z bodu H, se bude rovnat úhlu asymptot (z bodu H dohlédneme až k nevlastním bodům hyperboly právě ve směru asymptot). Jenže úhel asymtot nesouhlasí s úhlem uvedeným tazatelkou jako řešení. Takže já více neporadím.
Pokud se tedy nemýlím.
Offline
#7 29. 03. 2014 20:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Hyperbola
↑ Jj:
Také pozdrav, mne to už také zastavilo od psaní dalšího návodu, když byl dotaz kolegyňky ↑ Sheldon.C:, jelikož se mi to přestalo zdát. Ve sbírkách, co mám, jsem teď narychlo takovou úlohu nenašla - zda je v zadání překlep a bod H je mimo hyperbolu nebo něco jiného jinak.
↑ Sheldon.C: odkud je úloha? Děkuji.
Offline
#9 29. 03. 2014 21:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Hyperbola
↑ Sheldon.C:
Knihu jsem již našla - je tato, zadání souhlasí, ve výsledku však je 33 stupňů 12 minut. Což není tak podstatné.
Podstatné je, jak úlohu pojmout - zůstanu u myšlenky, že z bodu H mohu vidět jen druhou větev hyperboly, ne tu, na které bod H leží. Potom kolega ↑ Jj: navrhuje počítat odchylku asymptot. Ovšem měli bychom prokázat, že odchylka asymptot je totéž, co úhel, pod kterým vidíme hyperbolu z bodu H. Nějak nejsem si jistá celým postupem.
Offline
#10 29. 03. 2014 21:45
Re: Hyperbola
↑ jelena:
Ostrý úhel asymptot při přesnějším výpočtu vychází skutečně 33°12'.
Řekl bych, že máme-li z bodu H vidět právě celou druhou větev hyperboly, pak skutečně musí být ramena zorného úhlu rovnoběžná s asymptotami. V každé jiné poloze buď předmětnou větev hyperboly protnou, nebo se od ní vzdálí (jako např. "červená" tečna na obrázku výše).
Takže podle mne zorný úhel při pohledu z bodu H = ostrému úhlu asymptot.
Pokud se tedy nemýlím.
Offline
#11 29. 03. 2014 22:10 — Editoval vanok (29. 03. 2014 22:21)
Re: Hyperbola
Pozdravujem ↑ jelena:,↑ Jj:
Poznamka: pre kuzelosecky plati veta
Zo skutocneho( cize nie na kuzelosecke) vonkajsieho bodu kuzelosecky mame vzdy dve dotycnice na danu kuzelosecku.
Z bodu na kuzelosecke mame jedinu dotycnicu.
Z vnutorneho bodu nemame ziazdnu dotycnicu.
To moze byt pouzite na dany problem. ( co sa tyka druhej vetvy)
V probleme, tak ako je polozeny, treba uvazovat vsetki mozne priamky z daneho bodu, ktore pretinaju kuzelosecku... A preto ked sa pozerame na vetvu hyperboly ktoru vylucila ( asi nepravom) Jelena, mame rozpetie uhlov smernic priamok ktore pretinaju hyperbolu v tej vetve v rozpeti 180° ( vynimka je rovnobezna priamka z hlavnou osou hyperboly).
Cize zda sa mi, ze takyto problem potrebuje trochu casu na podrobnu analyzu vsetkych situacii ak by sme chceli vysetrit zvlast kazdu vetvu danej hyperboly. No ale ide o problem, podla cakanej odpovedi, v ktorom jeho autor ne analyzoval vsetki moznosti.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 29. 03. 2014 23:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Hyperbola
↑ Jj:
děkuji, ale to by neplatilo pro každou polohu bodu H na hyperbole (nemám na mysli polohu bodu H na hyperbole a zároveň na ose, ten je mi jasný). Zda to mohu tak zevšeobecnit pro každý bod?
↑ vanok:
také děkuji a ještě pozdrav. Není pěkné, že k řešení úlohy jdeme přes známý výsledek a také bychom v analytice neměli využívat obrázek.
Zkusím tedy úlohu přeformulovat tak: na hyperbole o známé rovnice najít bod X, který má minimální vzdálenost od tečny procházející bodem H. To mi dá jednu přímku HX, co bude vymezovat zorný úhel. Druhá přímka, která půjde bodem H, musí být rovnoběžná s asymptotou. Povede to k jednoznačnému řešení? Nebo to není správná formulace úlohy?
Mně to nijak nespěchá, mám i tak všeho teď moc, tak diskutujte, prosím, pomalu, děkuji :-)
Pravda: úhel 180 stupňů jsem také měla označit za zorný.
Sbírka, odkud je úloha, patří k těm lepším a spolehlivějším, tedy bych nepředpokládala nepořádné zadání.
Offline
#13 29. 03. 2014 23:36 — Editoval vanok (30. 03. 2014 00:08)
Re: Hyperbola
↑ jelena:,
Pozdravujem.
To aj tie najlepsie knihy maju z casu na cas nejaku chybu. Dokonalost to je ciel, ale...
Cakane riesenie sa tykalo druhej vetvy.
Vysledky co som napisal vysie sa pochopitelne daju dokazat aj analyticky.
Obrazky v podstate nie su podrebne v dokazoch, no vsak uzitocne na vybudovanie intuicii a potvrdenie toho, ze viacej ciest vedie k dokazu.
Aky nazor mal na to Descartes?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 30. 03. 2014 13:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Hyperbola
↑ vanok:
to jsem nechtěla říci, zda chybu/nechybu, ale nečekala bych v této knize nějakou metodickou nedokonalost nebo nejednoznačnost. A úlohy z tohoto typu sbírek obvykle si vystačí s využitím standardních kroků bez potřeby důkazu nad rámec probrané teorie. Zde bych nejdřív musela využit návrh důkazu kolegy ↑ Jj: (asi by šlo sepsat i důkaz přesně?). Jednoduše to v tématu mám(e) tak, že bez nabídky výsledku jsme standardní řešení nenapsali a to není seriózní. Souhlasíte?
Hyperbola má řádu optických vlastností, ale běžně se na SŠ neberou.
Aky nazor mal na to Descartes?
:-) zkusím se podívat (překlad do ruštiny mám, ale až bude klid a čas). I sem se podívám.
Offline
#15 30. 03. 2014 14:55
Re: Hyperbola
Pozdravujem ↑ jelena:,
Ta kniha od pana Vopenku si zasluzi byt precitana. Iste si ju obstaram.
Ten navrh od kolegu Jj je vyrok ku ktoremu som napisal vlastne len male doplnenie jeho tvrdenia. A jeho geometricky dokaz nas kolega prakticky vyjadril. ( jediny moj prinos je to, ze treba rozmyslat podla polohy daneho bodu, a tiez ze to plati pre vsetky kuzelosecky) Tento dokaz sa da urobit aj analyticky, co iste tu niekto doplni ( mozno aj ja ked budem mat na to cas)
Pochopitelne nevieme ake riesenie cakal autor knihy, ale je to pekne cvicenie na otvorene matematickeho ducha.
Descartes, to je len take male zmurknutie oka, ale je uzitocne studovat matematiku aj z historickeho pohladu.
Peknu nedelu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline


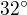 a 7 minut.
a 7 minut.