Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferencální rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 04. 2014 07:36 — Editoval Strabon (07. 04. 2014 07:38)
diferencální rovnice
Dobrý den, opět žádám o pomoc s příkladem. :(
Kdyby jste někdo znal nějaký pořádný materiál na diferencální rovnice, kde by bylo krásně všechno vysvětleno byl bych vděčný :)
Nevím jak na to :)
U diferencálních rovnic vím, že hledám homogení a partikulární řešení ... homogení řešení dělám přez separace proměných a partikulární přez variace a nebo přez metodu odhadu... To znám, ale tento příklad se mě právě ptá na něco a pořádně nevím na co... 
Offline
- (téma jako vyřešené označil(a) jelena)
#2 07. 04. 2014 10:24 — Editoval Rumburak (07. 04. 2014 10:26)
Re: diferencální rovnice
↑ Strabon:
Ahoj.
Zde není třeba řešení hledat, stačí pro každou z nabízených možností 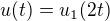 , ... atd. provést zkoušku dosazením
, ... atd. provést zkoušku dosazením
do levé strany rovnice a využít předpoklad o funkcích 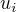 .
.
S dotazem na literaturu se obrať na vyučujícího, který nejlépe bude vědět, co se pro Tvůj kurs může hodit.
Offline
#3 07. 04. 2014 16:32
Re: diferencální rovnice
↑ Rumburak:
udělal bys prosím jedno vzorový řešení :) Jen pro jistotu :) děkuju
Offline
#4 07. 04. 2014 17:22
Re: diferencální rovnice
↑ Strabon:
Ještě připomínám, že množina všech řešení této rovnice tvoří lineární prostor (probírá se to v teorii),
takže ihned můžeme zaškrtnout druhou možnost.
Místo 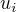 pišme
pišme  , abychom se neutopili v indexech a proberme třeba tu třetí možnost
, abychom se neutopili v indexech a proberme třeba tu třetí možnost 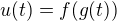 ,
,
která nemusí být úplně jednoduchá. Vypočtěme derivace této funkce  :
: ,
,  ,
,  .
.
Nyní sem dosaďme  , sestavme výraz
, sestavme výraz  a
a
zkoumejme rovnici  . Ale kam to povede, zatím netuším - očekávám výsledek
. Ale kam to povede, zatím netuším - očekávám výsledek  , ale teď už se musím věnovat něčemu jinému,
, ale teď už se musím věnovat něčemu jinému,
takže zkusím pokračovat zítra .
Offline
#5 07. 04. 2014 20:07
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: diferencální rovnice
ja bych pro to treti uvedl protipriklad, treba u_1=sin(x), u_2=cos(x).
U toho posledniho, tj. pro u(t-2) staci rozmyslet, jestli je rovnice autonomni.
Offline
#6 08. 04. 2014 09:27
Re: diferencální rovnice
↑ kaja.marik:
Zdravím a děkuji za doplnění, to nejjednodušší mne opravdu nenapadlo. :-(
Offline
#7 08. 04. 2014 15:17
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferencální rovnice (TOTO TÉMA JE VYŘEŠENÉ)
