Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 07. 04. 2014 19:17
Re: Nulové body kvadratické rovnice
Ahoj,
nulové body získáš že položíš daný předpis nule
vyzkoušíš pár čísel a zjistíš že x = 1 je řešením dané rovnice
vydělíš tedy celý polynom výrazem (x-1)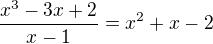
a následně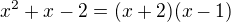
finální rozklad je tedy:
nulové body jsou tedy dva z toho jeden dvojnásobný, (ten ohyb se dotýká osy x v bodě 1).
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 07. 04. 2014 19:32
Re: Nulové body kvadratické rovnice
Kořen kubické rovnice můžeš získat tak, když její absolutní člen rozložíš na činitele, které zkoušíš dosadit do rovnice. V tvém případě je absolutním členem 2. Můžeš tedy zkoušet dosadit 1, -1, 2, -2.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 08. 04. 2014 08:50
Re: Nulové body kvadratické rovnice
↑ gadgetka:
Zdravím,
to co píšeš je pravda jenom pro celočíselné kořeny.
Offline
#6 09. 04. 2014 14:19
Re: Nulové body kvadratické rovnice
gadgetka napsal(a):
když její absolutní člen rozložíš na činitele, které zkoušíš dosadit do rovnice
:)  a můžeš zkoušet...
a můžeš zkoušet...
něco ti tam chybí, přesně jak řekl kolega ↑ Honzc:
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 09. 04. 2014 14:23
Re: Nulové body kvadratické rovnice
Ok, pánové, nebyla jsem přesná v odpovědi, to, co jsem měla v hlavě, jsem špatně vyjádřila... děkuji za opravu. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline

