Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » LA průnik zaměření (TOTO TÉMA JE VYŘEŠENÉ)
#2 13. 04. 2014 14:01
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: LA průnik zaměření
↑ skooty25:
Asi ti to moc nepomůže, ale není mi jasné, co je "zaměření". Ze scanu jsem pochopil snad jen to, že tam jde o ekvivalentní úpravy matice. Tj. asi by to chtělo formulovat nějak pochopitelnějc.
Offline
#3 13. 04. 2014 14:51
Re: LA průnik zaměření
Když máš zadanou třeba rovinu parametricky, takže A + t*u1 + s*u2, kde u1 a u2 jsou vektory, pak zaměření této roviny jsou právě tyto dva vektory...jinak vím, že tam je chyba pod upravenou maticí je napsáno (3,3,2,1) a má tam být (3,3,2,2), ale to v mojem problému nehraje žádnou roli
Offline
#4 13. 04. 2014 18:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LA průnik zaměření
↑ skooty25:
Zdravím, scan je hodně nečitelný a chybí tomu zadání. Lepší je přidávat odkaz na váš materiál (nebo čitelný scan materiálu), než převyprávění pojmů. Předpokládám, že jde o toto zadání - je tak? Děkuji.
Offline
#5 13. 04. 2014 20:17 — Editoval skooty25 (13. 04. 2014 20:25)
Re: LA průnik zaměření
ano, jde přesně o toto zadání, děkuji, tohle jsem tu nenašla asi jsem špatně vyhledávala, ale já vím jak dál počítat odchylku těch prostorů, ale nevím, jak vypočítat ten první krok, tedy průnik zaměření, kde vzal to (3,0,3,0) popřípadě (1,0,1,0), takže ono přesné zadání, co se má vypočítat, v tomhle vlastně nehraje roli, protože se mi jedná jenom o ten průnik, ale pro lepší přehled tu dám to zadání, co jste mi poslala, děkuji.

Offline
#7 13. 04. 2014 20:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LA průnik zaměření
↑ skooty25:
děkuji za upřesnění - hledáte lineární kombinaci směrových vektorů zadaných rovin (to je vytvořeno v 1. matici, sloupec 0 není zapsán). Úpravy k 2. matici jsem nekontrolovala. Zkus projít tento materiál str. 34 původního textu.
Offline
#8 14. 04. 2014 10:26 — Editoval skooty25 (14. 04. 2014 10:29)
Re: LA průnik zaměření
děkuju, tak už jsem myslela, že jsem to konečně pochopila z toho textu, ale když jsem to zkoušela pro jiný příklad, tak tam už zase nějak nevím co dělat protože je zadání takové, že ty vektory nejsou 2 a 2, ale 2 a 3. Posílám i zadání.
Určete odchylku vektorových podprostorů V a W zadaných jako lineární obal uvedeného souboru vektroů.![kopírovat do textarea $V=[(1,1,-2,1,-1), (1,-3,2,1,3)]$](/mathtex/bc/bc6468c8b7f5a100b94b9dc227a17b2a.gif)
![kopírovat do textarea $W=[(1,1,2,1,-1), (1,-3,-2,1,3), (1,-1,-3,-1,1)]$](/mathtex/94/94e63613038249ff0afb38047b29ae94.gif)
Offline
#9 14. 04. 2014 11:12
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: LA průnik zaměření
↑ skooty25:
Já to tak trošku analyzuju. Nejdřív bych radil si to představit nebo nakreslit, ale to může bejt ošidný... Věty bohužel stoprocentně neznám. Nicméně mi přijde, že tenhle případ jde řešit podobně.
O co jde: V je nadrovina ve 5D. Tj. má dimenzi 2.
W je "nadprostor" v 5D. Tj. má dimenzi 3 (teda pokud jsou 3 vektory lin. nezávislé, jinak je následující text jinak).
Jestli správně chápu lineární obal, tak V i W se potkávaj v nulovém vektoru.
(Kdyby byly "posunuté" tak by se potkat nemusely. Příklad ve 3D: rovina a přímka s ní rovnoběžná- jenže tady nemůžou jít oba nulovým vektorem).
Máš dál zjišťovat jejich průnik. Průnik je vektor a takovej, že jde vyjádřit jak v prvcích W, tak v prvcích V.
Tohle by tě mělo trknout, že tě vlastně zajímá řešení soustavy rovnic pro s,t,r,e,f s pravou stranou nulovým vektorem (odečte se pravá strana rovnice). Jinými slovy budeš mít matici 5x5 správně tvořenou těmi pěti vektory v zadání a děláš ekvivalentní úpravy.
Co může vyjít? pokud je všech pět vektorů lineárně nezávislých vyjde zas jenom nulový vektor jako řešení. Průnik je pak taky nulový vektor.
Dál si myslím, že může 2D rovina protínat 3D prostor v přímce- to se asi nedá představit. U rovnice to ale znamená řešení: s,t,r,e,f dává jeden směr a je určen až na velikost.
A konečně se může stát že 2D rovina leží celá v 3D prostoru, tím je průnik ta rovina a nejde určovat žádnou odchylku. Řešení rovnice bude "divné", vyjdou dva směry s,t,r,e,f které určují předešlou rovinu.
Offline
#10 14. 04. 2014 11:38 — Editoval skooty25 (14. 04. 2014 11:39)
Re: LA průnik zaměření
takže pokud to chápu dobře tak hodím do matice vektory z V a vektory z W akortá s opačným znaménkem (nebo naopak)?
takže když to hodím do matice mám tohle 
a po úpravách dostanu tohle (mělo by to být dobře, je to kontrolováno programem)
a teď jestli jsem to teda dobře pochopila tak z té matice by mělo jít vidět že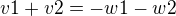 (kde v1, v2, w1, w2 jsou vektory)
(kde v1, v2, w1, w2 jsou vektory)
je to tak?
takže když heldám ten průnik tak stačí když udělám v1 + v2 a je hotovo?
Děkuji
Offline
#11 14. 04. 2014 18:18
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: LA průnik zaměření
Počáteční matice je v principu dobře. Pokud věřím těm ekvivalentním úpravám, tak už se jen dosazuje. Po dlouhý době mě vyšlo r=0, z předposledního řádku. A pak s=t=e=f= např. jedna. Takže je to skoro dobře, platí tohle, když s=1 :
A ten průnik je dobře. Případně jakékoliv (v1+v2)*p, p je reálné číslo.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » LA průnik zaměření (TOTO TÉMA JE VYŘEŠENÉ)

