Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 04. 2014 21:17
Monotonost funkce
Mám zadanou funkci: 
První derivace mi vyšla: 
Mám za úkol zjistit, v jakém intervalu je funkce rostoucí a klesající. Mám správně postup? Nebo se postupuje úplně jinak?
Děkuji moc za rady.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 20. 04. 2014 21:27 Příspěvek uživatele marnes byl skryt uživatelem marnes. Důvod: špatně
#4 20. 04. 2014 21:38 Příspěvek uživatele marnes byl skryt uživatelem marnes. Důvod: špatně
#5 20. 04. 2014 21:47 — Editoval Jj (20. 04. 2014 21:48)
Re: Monotonost funkce
↑ Matiniela:
Dobrý večer. Řekl bych, že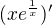 se, jak uvádíte, rovná
se, jak uvádíte, rovná 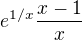 .
.
Dále nepočítáte správně (nerovnosti):
Pokud  , pak x-1 > 0 a x > 0 --> x > 1
, pak x-1 > 0 a x > 0 --> x > 1
nebo x-1 < 0 a x < 0 --> x < 0
Pokud  , pak x - 1 < 0 a x > 0 --> 0 < x < 1
, pak x - 1 < 0 a x > 0 --> 0 < x < 1
nebo x - 1 > 0 a x < 0 --> nemá řešení
Pokud se tedy nemýlím.
Offline
#8 20. 04. 2014 22:07
Re: Monotonost funkce
↑ Matiniela:
Jak jsem uvedl (nebo jinou metodou).
Výsledky:
a) Rostoucí pro (-oo, 0), (1,+oo)
b) Klesající pro (0,1)
Je-li proměnná ve zlomku Z v čitateli i jmenovateli, pak pro výpočet Z > 0 nebo Z < 0 nestačí počítat s čitatelem, ale nutno uvažovat také ovlivnění výpočtu znaménkem jmenovatele (které může obvykle být jak +, tak -).
Pokud se tedy nemýlím.
Offline
#10 20. 04. 2014 22:26
- marnes

- Příspěvky: 11227
Re: Monotonost funkce
své příspěvky jsem vymazal, měl jsem špatně derivaci - omluva
Jo. A na začátku vás zdravím.
Offline
#11 20. 04. 2014 22:35
Offline
#13 20. 04. 2014 22:54
Re: Monotonost funkce
↑ Matiniela:
Konvexní tam, kde je f''(x) > 0,
(konkávní naopak).
Pokud se tedy nemýlím.
Offline
#15 21. 04. 2014 08:42
Re: Monotonost funkce
↑ Matiniela:
Jak zjistit intervaly, kde je funkce konvexní (konkávní) jsem napsal tady ↑ Jj:.
Pokud se tedy nemýlím.
Offline
#17 21. 04. 2014 08:47
Re: Monotonost funkce
↑ Matiniela:
V podstatě ano (opačný případ, čitatel i jmenovatel menší než nula tu nepřichází v úvahu).
Pokud se tedy nemýlím.
Offline


