Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 22. 04. 2014 10:14
Re: Šikmá asymptota
Mám zadanou funkci : 
Mám vypočíst její asymptoty. Svislé asymptoty mám zbývá šikmá asymptota.
a) Podle vzorce f(x)/x jsem dosadil a vyšlo mi 1.
b) Do vzorce f(x)-ax jsem dosadil xe^1/x-1x. Vytkl jsem x a zbylo mi x(e^1/x-1), ale to je neurčitý výraz  *0 a nevím jak dále pokračovat.
*0 a nevím jak dále pokračovat.
Celý příklad má vyjít x+1
Offline
#4 22. 04. 2014 10:33
- janca361

- .
- Příspěvky: 3284
Re: Šikmá asymptota
Uáááá,
co jsou to "svislé asymptoty" a "šikmé asymptoty". Snad asymptoty bez směrnice a asymptoty se směrnicí.
Jste vysokoškolák, tak i vyjadřování by mělo být na úrovni, včetně používání termínů.
Offline
#7 22. 04. 2014 11:21
Re: Šikmá asymptota
↑ Matiniela:tak nedosadzuj ale počítaj limitu najjednoduchšie napríklad rozvojom exponenciály do Taylorovho radu alebo substitúciou 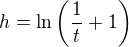 a využitím spojitosti logaritmu ale táto limita je dosť známa na to aby sa stále počítala
a využitím spojitosti logaritmu ale táto limita je dosť známa na to aby sa stále počítala
MATH IS THE BEST!!!
Offline

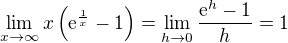
 a to znamena ze môzes pouzit L'hospitalovo pravidlo a citatela a menovadela samostatne poderivovat a ti to vide
a to znamena ze môzes pouzit L'hospitalovo pravidlo a citatela a menovadela samostatne poderivovat a ti to vide 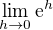 a to je 1
a to je 1