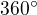Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 04. 2014 22:35
- bluestorman
- Zelenáč
- Příspěvky: 4
- Reputace: 0
Objem kuzele - prosím o pomoc
Dobrý den
Potřeboval bych pomoct s vyřešením následující úlohy:
Vyřešte následující problém:
Z menší části kruhové výseče s tupým středovým úhlem θ vystřižené z papírového kruhu o poloměru r je zhotoven kužel.
1. Vyjádřete objem tohoto kužele pomocí r a θ.
2. Pomocí substituce x = θ/2pi vyjádřete objem kužele jako funkci proměnné x.
3. Nakreslete graf této funkce a najděte hodnoty x a θ, pro které bude objem maximální; x vyjádřete na 4 desetinná místa.
Pokud vyřízneme z kruhu výseč, dostaneme výseče dvě a můžeme tak vyrobit dva kužele.
4. Najděte hodnotu nebo hodnoty x, pro kterou (pro které) bude součet objemů obou kuželů maximální.
Offline
- (téma jako vyřešené označil(a) bluestorman)
#2 27. 04. 2014 22:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Objem kuzele - prosím o pomoc
Zdravím,
téma jsem přesunula do SŠ, kam patři. Úloh s kuželem (i tato) je zde více - zkus pohledat. Jinak nekonkretizuješ, s čím potřebuješ pomoct - začni obrázkem, který zde můžeš umístit a upřesní - co je konkrétně problém viz pravidla - bod 3. Děkuji.
Offline
#3 27. 04. 2014 23:49
- bluestorman
- Zelenáč
- Příspěvky: 4
- Reputace: 0
Re: Objem kuzele - prosím o pomoc
Jo, omlouvám se ohledně zařazení. Potřeboval bych kompletní řešení dané úlohy, bod po bodu.
Offline
#4 28. 04. 2014 09:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Objem kuzele - prosím o pomoc
↑ bluestorman:
účelem fóra není poskytování kompletních řešení. Pokud se chceš na řešení aktivně podílet, potom ano, lze pokračovat - začni obrázkem, potom rozbor zadání, rozbor požadavků jednotlivých podúloh atd. Jinak označ téma za vyřešené a zkus se podívat po nabídkách hotových řešení od firem, co se tomu věnuji.
Děkuji za pochopení.
Offline
#5 28. 04. 2014 09:51
Re: Objem kuzele - prosím o pomoc
↑ bluestorman:
Ahoj. Zkus na to jít z druhé strany: uvažuj kužel a "rozbal" jeho plášť do kruhové výseče.
Offline
#6 29. 04. 2014 09:59 — Editoval Honzc (29. 04. 2014 10:05)
Re: Objem kuzele - prosím o pomoc
↑ bluestorman:
Ta úloha se mi zdá, alespoň co se týká tohoto "Z menší části kruhové výseče s tupým středovým úhlem θ... ", a potom výpočtu bodu 3, nesmyslně zadaná. No nicméně.
Trochu ti napovím: (to tvé 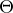 si označím
si označím  , a připomínám, že je potřeba počítat v obloukové míře)
, a připomínám, že je potřeba počítat v obloukové míře)
a) délka oblouku kružnice o poloměru  nad středovým úhlem
nad středovým úhlem  se musí rovnat obvodu podstavy kuželu, který z té výseče "stočíš".
se musí rovnat obvodu podstavy kuželu, který z té výseče "stočíš".
b) tak můžeš určit poloměr podstavy kuželu (označme ho třeba  )
)
c) z osového řezu tímto kuželem a pomocí Pythagorovy věty spočítáš výšku kuželu (délka površky -strany kuželu je přitom samozřejmě  )
)
d) z těchto údajů a vzorečku určíš objem kuželu
Tím máš vyřešeny body 1) a 2)
A teď k bodu 3. (bez počítání) - obecně musí platit:
Je jasné, že pokud bude středový úhel blízký nule pak poloměr kuželu, který z něho můžeš stočit se bude blížit nule a tedy i objem se bude blížit nule. Naopak, pokud se středový úhel bude blížit 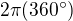 , pak zase výška se bude blížit nule a také objem se bude blížit nule.
, pak zase výška se bude blížit nule a také objem se bude blížit nule.
To tedy znamená, že funkce (objemu) závislá na  bude pro hodnoty
bude pro hodnoty  a
a  nulová.
nulová.
Ani nemusíš znát předpis té funkce, abys podle Rolleovy věty mohl vyslovit hypotézu, že maximální objem (objem je kladné číslo) bude někde mezi krajními hodnotami 
Dále už pohledem zjistíš, že maximum leží někde za  což odpovídá středovému úhlu
což odpovídá středovému úhlu 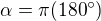 a tedy proto, to nesmyslné zadání a největší objem bude, když se
a tedy proto, to nesmyslné zadání a největší objem bude, když se  bude blížit
bude blížit 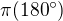
Pokud by nebyl v zadání požadavek na stočení menší výseče (tupý úhel) pak vysledek je
K bodu 4)
To není vůbec snadné a předpokládá to znát numerické metody řešení rovnic
Offline
#7 29. 04. 2014 11:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Objem kuzele - prosím o pomoc
↑ Honzc:
Zdravím,
proč se od vás nikdy nedočkám v příslušné sekci vyjádření k otázce kompletních řešení - že chcete fórum jiné a jinak - vždyť se to snad dá pokusit zdůvodnit? Místo toho se dočkám přidání příspěvku v tématu, kde jsem jasně napsala podmínky, za kterých téma bude diskutováno. Ovšem já se nedočkám ani drobné poznámky k příspěvku ↑ č. 4:.
Je to úloha, která je součást splnění podmínek předmětu, podrobněji zatím nevím. Tedy různé rozbory a náměty učitel očekává od kolegy (a zde na fóru je očekáváno dle pravidla 3).
K bodu 2 a 3 - řekla bych, že to je jen trochu umělý krok, jak ze zadání dostat pryč úhel  a převést úlohu na "hledání extrému funkce f(x)". Závěrečný výpočet se předpokládá s využitím počítačů.
a převést úlohu na "hledání extrému funkce f(x)". Závěrečný výpočet se předpokládá s využitím počítačů.
Tož pozdrav (i bratrovi) :-)
Offline
#9 29. 04. 2014 13:52
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Objem kuzele - prosím o pomoc
↑ Honzc:
:-) jsi pochyboval o zbytku účastníků tématu, že za předpokladu, že by se kolega rozhodl pokusit svůj problém řešit aktivně, tak bychom ho v tom nechali samotného? Zatím ale o téma nejevil zájem, tlapku o tlapku neudeřil, tak abychom se zbytečně nenamáhali. Přeci ten rozbor mu dá nejvíce, teď je o všechno ochuzen.
Pravda, o mně jsi pochyboval správně - vidím v tématu kolegu ↑ Rumburak:, tak v první řadě nesmím zapomenout dohledat, co Karolína psala o kornoutech :-)
Offline
#10 29. 04. 2014 15:17
- bluestorman
- Zelenáč
- Příspěvky: 4
- Reputace: 0
Re: Objem kuzele - prosím o pomoc
Děkuji všem, kteří mi pomohli k vyřešení problému. Co se týče pravidel,omlouvám se, že jsem si je nepřečetl. Potřeboval jsem pomoci co nejrychleji a to se mi i splnilo. K večeru sem nahraju mé řešení, aby mohlo být napomocno popřípadě ostatním. Sem na foru prvně a nebyl čas na řešení pravidel. Tímto tedy ještě jedna omluva a nadále již budu vše přechozí považovat za samozřejmost. Děkuji za pomoc.
Offline

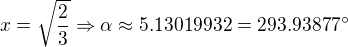
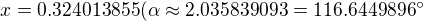 a druhý úhel doplněk do
a druhý úhel doplněk do