Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 02. 05. 2014 12:53
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
16.
Řešení:
Počet možných jevů: 6
16.1
Příznivé jevy: 2, 4, 6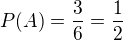 - ANO
- ANO
16.2
Příznivé jevy: 5, 6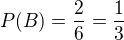 - NE
- NE
16.3
Příznivé jevy: 1, 2 - ANO
- ANO
16.4
Příznivé jevy: 1, 2, 3, 4, 5 - NE
- NE
Offline
#28 02. 05. 2014 12:55 — Editoval janca361 (02. 05. 2014 13:20)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
18.
Řešení:
x...počet výrobků 1. kvality
y...počet výrobků 3. kvality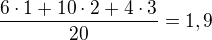
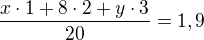

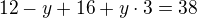

D
Díky Crashatorr za řešení!
Offline
#31 02. 05. 2014 13:00 Příspěvek uživatele ales2q byl skryt uživatelem janca361.
#34 02. 05. 2014 13:02 Příspěvek uživatele janca361 byl skryt uživatelem janca361.
#35 02. 05. 2014 13:02 Příspěvek uživatele ales2q byl skryt uživatelem janca361. Důvod: Řešení doplněno, další budou taky. Je zbytečné se na ně ptát.
#37 02. 05. 2014 13:05 — Editoval Crashatorr (02. 05. 2014 13:12) Příspěvek uživatele Crashatorr byl skryt uživatelem janca361. Důvod: Doplněno k danému zadání. Děkuji!
#39 02. 05. 2014 13:07
- VanilkaBanan

- Zelenáč
- Příspěvky: 6
- Reputace: 0
Re: Řešení maturitního testu jaro 2014
↑↑ janca361:↑↑ janca361: k tomu trojúhelníku ale známe obsah PLM ne KLM a máme spočítat PM a ne KM. Nebo jsem něco nepochopila?
Offline
#40 02. 05. 2014 13:07 — Editoval janca361 (02. 05. 2014 13:39)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
25.
Řešení:
25.1

E
25.2


D
25.3

A
25.4
F
Offline
#41 02. 05. 2014 13:24
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
↑ VanilkaBanan:
KL je výška na stranu PM v trojúhelníku PLM.
Offline
#42 02. 05. 2014 14:09
Re: Řešení maturitního testu jaro 2014
Zde http://jdem.cz/ba2xu6 (FB vlákno) jsou moje výsledky. Jsem si jimi docela jistý, tak kdyžtak pro kontrolu :-)
Fyzika a matematika konečně srozumitelně - www.nabla.cz
Fyzikální bludy
Řešení státní maturity z matematiky
Kdy psát mě a mně
Offline
#43 02. 05. 2014 14:11 Příspěvek uživatele Kelly18 byl skryt uživatelem janca361. Důvod: Doplněno
#44 02. 05. 2014 14:18 Příspěvek uživatele honza1994 byl skryt uživatelem janca361. Důvod: Doplněno
#46 02. 05. 2014 14:41 Příspěvek uživatele veru.19 byl skryt uživatelem janca361. Důvod: Všechny uvedené příklady jsou tu vyřešeny.
#47 02. 05. 2014 16:00 Příspěvek uživatele janca361 byl skryt uživatelem janca361.
#48 02. 05. 2014 16:32
Re: Řešení maturitního testu jaro 2014
Mohl bych mít prosím dotaz?
Když jsem si bohužel neuvědomil u úlohy číslo 4 v jakém definičním oboru se úloha řeší a napsal jsem zde podmínky, bude mi stržen bod?
A ještě jeden dotaz, u jedné úlohy jsem nedosadil za pí - napsal jsem místo 11 litrů 3,5pí litru. Bude mi výsledek uznán?
Moc děkuji za odpovědi!
Offline
#49 02. 05. 2014 16:40
Re: Řešení maturitního testu jaro 2014
Tak jsem to řešení přepsal, přehledně na jednu stránku. Snad bych maturitu udělal :-)
http://www.nabla.cz/obsah/matematika/statni-maturita/
Fyzika a matematika konečně srozumitelně - www.nabla.cz
Fyzikální bludy
Řešení státní maturity z matematiky
Kdy psát mě a mně
Offline
#50 02. 05. 2014 16:55
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
↑ Buránek:
Na odpověď k otázce by ti asi nejlíp odpověděl nějaký hodnotitel.
Osobně nevím. Tuším, že se říkalo, že pokud je něco uvedené jako řešení a je to špatně, tak je to chyba. (Proto se má psát jen to, co zadání vyžaduje.)
Chvíli jsem nad tím taky váhala, ale CERMAT (jak jsem ze starších testů zjistila) na podmínky buď upozorňuje (v zadání je "stanovte podmínku řešení" viz úloha č. 5) nebo je sám zapisuje (Např. proveďte pro  - zde pro
- zde pro 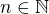 )
)
Jde o to, že  a o
a o  se nedá mluvit - o té nule jo (celá vs přirozená čísla - kam jen ta nula patří?)
se nedá mluvit - o té nule jo (celá vs přirozená čísla - kam jen ta nula patří?)
Bude záležet na pokynech pro hodnotitele. (Údajně k jednomu příkladu je x stránek toho, jak postupovat.)
V 15.2 je nedosazení za  OK, pokud by bylo "zaokrouhlete na celé litry", tak je to chyba.
OK, pokud by bylo "zaokrouhlete na celé litry", tak je to chyba.  je číslo,
je číslo, 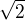 taky.
taky.
Já třeba nemám ve zvyku za takové čísla dosazovat 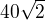 je pro mě stejně hezké číslo jako 361. Naopak napsat místo
je pro mě stejně hezké číslo jako 361. Naopak napsat místo 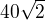 číslo
číslo  je blbost (a spousta lidí to ještě blbě zaokrouhluje). Ideálně s takovým číslem počítá dál a pak jsou vidět rozdíly. Ostatně já raději než s čísly počítám obecně.
je blbost (a spousta lidí to ještě blbě zaokrouhluje). Ideálně s takovým číslem počítá dál a pak jsou vidět rozdíly. Ostatně já raději než s čísly počítám obecně.
Offline








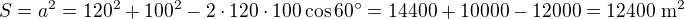

![kopírovat do textarea $S_{BC}[3;2]$](/mathtex/95/958f6746104622baede8e72feb1b8200.gif)