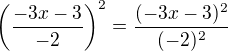Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Rovnice s neznámou pod odmocninou (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 05. 2014 10:43
Rovnice s neznámou pod odmocninou
Dobrý den, potřeboval bych poradit, kde dělám chybu:
Příklad: 
Můj postup:
1) umocním to celé na druhou (vznikne jedna odmocnina)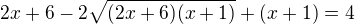
2)poté posčítám a roznásobím to co je v pod odmocninou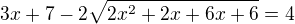
3)nechám odmocninu samotnou a vše ostatní převedu na druhou stranu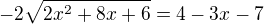
4)vydělím to (-2)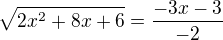
5)můj další postup by byl takový, že bych to umocnil na druhou
A teď jsem v koncích nevím jak dál :(
Výsledek má být 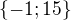
Předem děkuji za pomoc. :)
Offline
- (téma jako vyřešené označil(a) flagman)
#2 10. 05. 2014 10:53
Re: Rovnice s neznámou pod odmocninou
↑ flagman:
Dobrý den, řekl bych, že je vhodné výraz
před umocněním převést na pravou stranu rovnice.
Pokud se tedy nemýlím.
Offline
#3 10. 05. 2014 10:55
- janca361

- .
- Příspěvky: 3284
Re: Rovnice s neznámou pod odmocninou
↑ flagman:
Pokud je to OK (nekontrolovala jsem postup), tak znovu umocnit.
Jinak předpokládám, že budeš na závěr dělat zkoušku, která je zde nutná, protože na začátku si nenapsal podmínky. (Není to chyba, dokonce se říká, že zkouška je jednodušší - ovšem u nerovnic narazíš, tam zkoušku provést nelze)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Rovnice s neznámou pod odmocninou (TOTO TÉMA JE VYŘEŠENÉ)