Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 05. 2014 11:58 — Editoval ajsiivinr (14. 05. 2014 12:38)
limity
Zdravím všechny a prosím o radu ohledně výpočtu těchto limit:

první má vyjít  a druhá
a druhá 
u té druhé jsem došla vytknutím 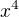 v čitateli a x ve jmenovateli k tomuhle:
v čitateli a x ve jmenovateli k tomuhle: to se rovná
to se rovná 
a teď tam mám za x dosadit mínus nekonečno? bude se při umocnění chovat stejně jako obyčejné záporné číslo?
u té první jsem před závorku vytkla  to znamená:
to znamená:
pak jsem závorku usměrnila:
x^2 se pokrátí a zbyde :
a teď mě zajímá stejná věc, nahoře bude nekonečno, dole odmocnina z nekonečna + nekonečno?...díky
Offline
#2 14. 05. 2014 12:07
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: limity
↑ ajsiivinr: Stačí takhle? 
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#3 14. 05. 2014 19:14
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: limity
Ahoj,
mohl bych se jen ze zvědavosti zeptat, proč se v prvním vytýkalo  ?
?
Nešlo by to rovnou usměrnit?
Offline
#4 14. 05. 2014 23:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limity
↑ cutrongxoay:
Zdravím, šlo by nejdřív usměrnit a potom vytknout x v jmenovateli (zde bez absolutní hodnoty, jelikož x jde k +oo), tedy rovnou krok kolegy ↑ Anonymystik:.
šlo by nejdřív usměrnit a potom vytknout x v jmenovateli (zde bez absolutní hodnoty, jelikož x jde k +oo), tedy rovnou krok kolegy ↑ Anonymystik:.
Offline
#6 15. 05. 2014 18:56
Re: limity
↑ cutrongxoay:
Ze zvědavosti:D
Jasně, je to zbytečný krok, úplně nevím, proč jsem to dělala, asi jsem si chtěla procvičit vyrábění výrazů v LaTeXovém editor:D:D Díky za upozornění...
Offline