Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 05. 2014 13:39
Jak na tuto kvad.nerovnici ?
Ahoj,chci se zeptat , dostali jsme příklad  a máme udělat osu,na ní vyznačit body a zapsat tam +,- a nakonec výsledek ... (tohle je graf toho příkladu v malování,bylo to narychlo,takže o krásu nejde :D)
a máme udělat osu,na ní vyznačit body a zapsat tam +,- a nakonec výsledek ... (tohle je graf toho příkladu v malování,bylo to narychlo,takže o krásu nejde :D) 
Chápu vše až na jedno ... jak poznám , že tam má být + - + a né třeba - + - ? Učitel říkal , že jak určím porvní znaménko na levé straně,tak pak se to jen střídá ... (někdy ne,ale to neděláme). Takže se chci jen zeptat,jak poznám,jeslti tam mám dát +,nebo - ? Díky
Offline
#2 22. 05. 2014 13:50
Re: Jak na tuto kvad.nerovnici ?
↑ robobobo:
Stačí si dosadit nějaké číslo z daného intervalu, např:
Výsledek je kladný, proto bude na prvním intervalu 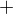
Stejně tak si můžeš dosadit třeba z druhého intervalu:
Výsledek je záporný, na daném intervalu tedy bude 
Offline
#3 22. 05. 2014 13:53
Re: Jak na tuto kvad.nerovnici ?
↑ runcorne:
Aha,tak díky a jen dotaz,pokud Diskriminant výjde záporný a parabola se tím pádem nebude dotýkat osy,tak výsledek je P=R ?
Offline
#4 22. 05. 2014 14:07
- misaH
- Příspěvky: 13460
Re: Jak na tuto kvad.nerovnici ?
↑ robobobo:
Ide o smer nerovnosti. Niekedy je P=R A niekedy prázdna množina.
Offline
#5 22. 05. 2014 14:13
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Jak na tuto kvad.nerovnici ?
Ahoj,
1) vycist z grafu, pokud vis ze "a" je kladne, tak graf bude konvexni, takze si jen predstavit graf a je to
2) zjistit nulove body, v tomto pripade jsou 2 body nulove, tim padem existuji 3 intervaly. V intervalech zvolis zkusebni bod a dosadis do vyrazu ...viz /runcorne
Offline
#7 22. 05. 2014 17:30
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Jak na tuto kvad.nerovnici ?
↑ robobobo:
Ja z toho obrazku vidim, ze pro "x" nesmi byt -1 i +1
Definicni obor je sjednoceni intervalu, jsou jasne videt 
Offline
#8 22. 05. 2014 19:45
Re: Jak na tuto kvad.nerovnici ?
↑ cutrongxoay:
a to nemusí být sjednoceny všechny čtyři ? Já myslel,že pokud se nikde nesjednotí všechny,tak to nejde
Offline
#9 22. 05. 2014 22:33
- misaH
- Příspěvky: 13460
Re: Jak na tuto kvad.nerovnici ?
↑ robobobo:
Pôvodnú úlohu nepoznám, ale všeobecne:
Definičný obor obsahuje všetky čísla, pre ktoré sa dá vyrátať hodnota uvažovaného výrazu. Celého.
Čísla, ktoré vyhovujú iba jednej časti výrazu nemôžu teda do D ( f ) patriť.
Offline

