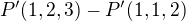Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 05. 2014 16:26
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Permutace
Poprosil bych opet pomoc s jednim prikladem
Určete počet anagramů, které lze získat ze slova ROKOKO, jestliže v nich nesmí být všechna tři písmena O vedle sebe
Skoncil jsem tady 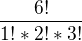 a dal uz nevim, jak bych mel do toho zapojit i podminku.
a dal uz nevim, jak bych mel do toho zapojit i podminku.
Predem diky
Offline
#3 24. 05. 2014 17:04
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Permutace
↑ gadgetka:
a co to prosim znamena. jestli se mohu zeptat?
Offline