Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Geometrie - konstrukce trojuhelníku (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 05. 2014 18:32
Geometrie - konstrukce trojuhelníku
Ahoj, přiznám rovnou - je to úkol, ale zasek jsem se u něj na několik hodin a nic mě nenapadá
zadání zní: Sestrojte trojuhelník s danou stranou c (AB), úhlem  a poloměrem kružnice vepsané. Jediné, na co jsem vlastně přišel je, že to bude příklad na otáčení... a možná i posunutí? Začnu tím úhlem, pak udělám osu, vrazím tam kružnici a dál už nevim... dá se využít fakt, že ta osa rozdělí stranu c přesně napůl?
a poloměrem kružnice vepsané. Jediné, na co jsem vlastně přišel je, že to bude příklad na otáčení... a možná i posunutí? Začnu tím úhlem, pak udělám osu, vrazím tam kružnici a dál už nevim... dá se využít fakt, že ta osa rozdělí stranu c přesně napůl?
Offline
- (téma jako vyřešené označil(a) Indiik)
#3 27. 05. 2014 19:07
Re: Geometrie - konstrukce trojuhelníku
Zdravím. Myslím si, že takhle jednoduše to nejde (Baky), respektive nerozumím tvému postupu. (neznáš dotykový bod). Takovýhle trojúhelník se podle mne musí dělat trošku jinak. Označím S střed kružnice vepsané, spočítám úhel ASB a zbytek snadno doděláš.
k zadavateli, také mne v první chvíli napadlo otočení/ stejnolehlost, bohužel mne však nenapadá jak.
// moc se mi nelíbí to počítání, tak bych rád přečetl řešení, kdyby někoho napadlo bez výpočtu.
Offline
#7 27. 05. 2014 19:33 — Editoval Indiik (27. 05. 2014 19:39)
Re: Geometrie - konstrukce trojuhelníku
asi jsem tupec, ale nerozumim ti, ten úhel je přeci při každým jiným sklonu té strany c - jiný... jinak ta gama je jak si jí zvolim
navíc teda nechápu jak mi spočítanej úhel ASB pomůže ke konstrukci...?
Offline
#12 27. 05. 2014 20:21
Re: Geometrie - konstrukce trojuhelníku
Ne, není to 2 gama
máš 2 rovnice 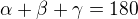
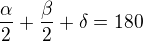
první upravíš na :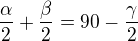
alfa půl + beta půl dosadíš do 2.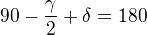
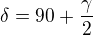
delta je úhel při S
Takže máš trojůhelník ABS, kde znáš stranu AB, výšku na stranu AB a úhel při S.
Uděláš tedy AB, potom GMB úhlu delta, potom rovnoběžku s AB ve vzdálenosti ró (poloměr kružnice vepsané), kde se ti protne s GMB delta vznikne ti střed kružnice vepsané (pro obecnost vol tak, aby vznikla 2 řešení). Uděláš kružnici a k ní tečny z bodů A a B, kde se ti protnou vznikne bod C (2 řešení)
Ok?
Offline
#15 27. 05. 2014 22:17
Re: Geometrie - konstrukce trojuhelníku
začínáš taky tou stranou c, uděláš trojuhelník s úhlem 2  tím získáš ten střed, dále uděláš kružnici se středem v s o poloměru sA - to je kružnice, která je opsaná tomu našemu hledanému trojuhelníku, pak udělám opsanou tomu menšímu ABS - kamarád mi vysvětlil (důkaz tedy nevím) že to je vlastně kružnice na kterých leží všude středy vepsaných kružnic, které budou mít u vrcholu C velikost úhlu gama. Takže máš danou stranu a máš danej úhel, zbývá najít dva body na té opsané kružnici, která má požadovaný poloměr.
tím získáš ten střed, dále uděláš kružnici se středem v s o poloměru sA - to je kružnice, která je opsaná tomu našemu hledanému trojuhelníku, pak udělám opsanou tomu menšímu ABS - kamarád mi vysvětlil (důkaz tedy nevím) že to je vlastně kružnice na kterých leží všude středy vepsaných kružnic, které budou mít u vrcholu C velikost úhlu gama. Takže máš danou stranu a máš danej úhel, zbývá najít dva body na té opsané kružnici, která má požadovaný poloměr.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Geometrie - konstrukce trojuhelníku (TOTO TÉMA JE VYŘEŠENÉ)

 a stred kružnice vpísanej, tak trojuholník z nich vieš zostrojiť.
a stred kružnice vpísanej, tak trojuholník z nich vieš zostrojiť.
 .
.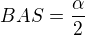 , protože AS je osa úhlu, stejně pro ABS a využiješ, že v trojúhelníku je součet úhlů 180
, protože AS je osa úhlu, stejně pro ABS a využiješ, že v trojúhelníku je součet úhlů 180