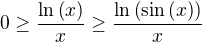Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Májový nevlastní integrál (snadnější)
#2 06. 05. 2010 20:04 — Editoval Pavel (06. 05. 2010 20:06)
Re: Májový nevlastní integrál (snadnější)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 07. 05. 2010 23:23
Re: Májový nevlastní integrál (snadnější)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#5 21. 03. 2011 10:49
Re: Májový nevlastní integrál (snadnější)
↑ Pavel:
Srdečně zdravím !
Vtipně vyřešeno, jen si dovolím doplnit jednu maličkost.
PS. Že reaguji až nyní bylo způsobeno tím, že toto téma původně uniklo mé pozornosti a teprve nedavno bylo připomenuto jinou úlohou.
Offline
#6 21. 03. 2011 17:56 — Editoval Pavel (21. 03. 2011 17:57)
Re: Májový nevlastní integrál (snadnější)
↑ Rumburak:
Máš samozřejmě pravdu, výpočet byl opravdu založen na předpokladu, že integrál existuje a je konečný. Nyní k samotnému důkazu.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 23. 03. 2011 10:33 — Editoval Marian (23. 03. 2011 10:40)
Re: Májový nevlastní integrál (snadnější)
↑ Pavel:↑ Rumburak:
Našel jsem také jednu možnost jak dokázat existenci nevlastního integrálu v původním zadání. Protože se metoda dosti liší od Pavlova přístupu, uvedu ji níže.
Offline
#9 23. 03. 2011 16:36
Re: Májový nevlastní integrál (snadnější)
↑ Marian:
Tak to už je matematický koncert :-) - rozhodně poučný.
Můj způsob důkazu existence a konečnosti integrálu i výpočtu jeho hodnoty byl v klíčových myšlenkách shodný s Pavlovým, takže ho neuvádím.
Offline
#10 11. 06. 2014 13:40
Re: Májový nevlastní integrál (snadnější)
Pozdravujem, dovolim si pridat len male doplnky:
Co sa sa tyka konvergencie integralu, v okoli 0, mozno pouzit, ze 
Este pridam, ze ak napiseme  ( oznacenie ako ↑ Pavel:) vo forme
( oznacenie ako ↑ Pavel:) vo forme  mozeme ho vypocitat aj vo forme radu, vdaka rozvoju logaritmu v okoli 1.
mozeme ho vypocitat aj vo forme radu, vdaka rozvoju logaritmu v okoli 1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 12. 06. 2014 21:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Májový nevlastní integrál (snadnější)
Zdravím,
z tématu dle prosby kolegy vanok vyčleněna diskuse k integrálu tvaru
příklady  a
a  jsou ve sbírkách.
jsou ve sbírkách.
jarrro napsal(a):
pri nekladných funkciách platí trochu obrátené porovnávacie kritérium teda ak väčší integrál diverguje tak diverguje aj menší
problém je len u nuly teda stačí skúmať
teda musí aj pôvodný sínusový divergovať lebo na (0,1) je
Dia napsal(a):
ta limita by mala vyjst +
, lebo ked sa blizi k nule tak ln sa blizi do -
, ci? v kazdom pripade velmi pekne dakujem to o tych zapornych integraloch som nevedela
Marian napsal(a):
↑ jelena:
Situace týkající se integrálu
kde, se má takto:
1. prokonverguje,
2. prodiverguje do
.
V obojím případě lze provést odhady zadaného integrálu pomocí nerovnosti
Odtud dostaneme nerovnosti
ad 1. Prointegrál zcela vpravo diverguje do
, odkud již plyne divergence původního integrálu (také do
).
ad 2. Proje integrál zcela vlevo konvergentní, odkud plyne omezenost původního integrálu (horním ohraničením je třeba nula). Odtud už není těžké odvodit jeho konvergenci (stačí využít monotonie integrandu na pozorovaném intervalu).
Postupovat je ale možno i podobně, jak je uvedeno v příspěvcích již dávno zapomenutého tématu o "májovém integrálu" zde.
Rumburak napsal(a):
Ahoj vespolek.
Je to ještě jednodušší. Předpokládejme, že. Odtud postupně
,
,
.
Z posledního odhadu je divergence integrálu

již patrná.
--------
"Problém podobného typu již zde v zajímavých úlohách z matematické analýzy byl" (c)
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Májový nevlastní integrál (snadnější)


 , mohu psát
, mohu psát
![kopírovat do textarea $ \Large I=2\int_{0}^{\pi/2}\ln (\sin (x))\,\mathrm{d}x= 2\int_{0}^{\pi/2}\ln (2\sin (x/2)\cos(x/2))\,\mathrm{d}x=\nl =2\int_{0}^{\pi/2}\ln 2+\ln(\sin (x/2))+\ln(\cos(x/2))\,\mathrm{d}x=\nl =2\int_{0}^{\pi/2}\ln 2\,\text{d}x+2\int_{0}^{\pi/2}\ln(\sin (x/2))\,\text{d}x+2\int_{0}^{\pi/2}\ln(\cos(x/2))\,\text{d}x=\nl =\pi\ln 2+2\int_{0}^{\pi/2}\ln(\sin (x/2))\,\text{d}x+2\int_{0}^{\pi/2}\ln(\sin(x/2+\pi/2))\,\text{d}x=[\text{subst. }x/2+\pi/2=t/2]\nl =\pi\ln 2+2\int_{0}^{\pi/2}\ln(\sin (x/2))\,\text{d}x+2\int_{\pi/2}^{\pi}\ln(\sin(t/2))\,\text{d}t=\nl =\pi\ln 2+2\int_{0}^{\pi}\ln(\sin (x/2))\,\text{d}x=[\text{subst. }x/2=u]\nl =\pi\ln 2+4\int_{0}^{\pi/2}\ln(\sin (u))\,\text{d}x=\pi\ln 2+2I. $](/mathtex/46/462a11ee99f584d24d595bb40389fa7f.gif)

 nelze vyjádřit konečným počtem elementárních funkcí.
nelze vyjádřit konečným počtem elementárních funkcí.

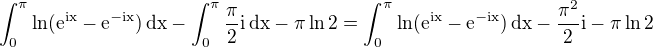

 . Potom by sme dostali, že pôvodný integrál je
. Potom by sme dostali, že pôvodný integrál je
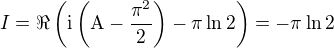
 , je mlčky postaveno na předpokladu, že hodnota integrálu I je konečná.
, je mlčky postaveno na předpokladu, že hodnota integrálu I je konečná.  je sudá kolem
je sudá kolem  , ukážu, že je konvergentní integrál
, ukážu, že je konvergentní integrál 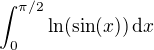
 . Protože
. Protože ![kopírovat do textarea $\sin x\in(0,1]$](/mathtex/c3/c3acdbe9acde3bdc38061adf6b71c229.gif) pro
pro ![kopírovat do textarea $x\in[\delta,\pi/2]$](/mathtex/94/94d33203074e8c62d7c7ee80298da50d.gif) , platí pro tato
, platí pro tato  , že
, že  a také
a také  . Integrál je tedy omezený shora. Ukažme, že je omezen i zdola.
. Integrál je tedy omezený shora. Ukažme, že je omezen i zdola.
![kopírovat do textarea $\frac{\sin x}{x}\in[2/\pi,1]$](/mathtex/66/663bd6244611bb6d1ffea2205e353f5c.gif) pro
pro ![kopírovat do textarea $x\in[0,\pi/2]$](/mathtex/61/61ff93ae546eb75456d862bcf80ea9cd.gif) .
.![kopírovat do textarea $&\int_{\delta}^{\pi/2}\left(\ln x+\ln\frac{\sin x}x\right)\text{d}x>\int_{\delta}^{\pi/2}\left(\ln x+\ln\frac{2}{\pi}\right)\text{d}x=\left[x\ln x-x+x\ln\frac{2}{\pi}\right]_{\delta}^{\pi/2}=\\
&=\frac{\pi}{2}\ln\frac{\pi}{2}-\frac{\pi}{2}+\frac{\pi}{2}\ln\frac{2}{\pi}-\delta\ln\delta+\delta-\delta\ln\frac 2{\pi}=-\frac{\pi}{2}-\delta\ln\delta+\delta-\delta\ln\frac{2}{\pi}.$](/mathtex/da/da0a68fb331032ff6dbb2a4a9e376cc8.gif)
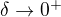 dokážeme, že původní integrál je konvergentní.
dokážeme, že původní integrál je konvergentní.
 . Ukážeme nyní omezenost nevlastního integrálu.
. Ukážeme nyní omezenost nevlastního integrálu.




 dostáváme pro předchozí limitu vztah
dostáváme pro předchozí limitu vztah

 je fixní záporná konstanta, která existuje, neboť uvedená nekonečná řada konverguje stejně rychle jako nekonečná řada
je fixní záporná konstanta, která existuje, neboť uvedená nekonečná řada konverguje stejně rychle jako nekonečná řada 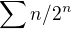 .
.![kopírovat do textarea $\lim_{a\to0^{+}}\int_{a}^{1}\frac{lnx}{x}dx=\lim_{a\to 0^{+}}{\[\frac{\ln^2{x}}{2}\]_a^1}=\lim_{a\to 0^{+}}{0-\frac{\ln^2{a}}{2}}=-\infty$](/mathtex/ae/aeb093ec7fd3e6af93e55b1927d49d48.gif)