Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 07. 2014 12:18 — Editoval o.neill (05. 07. 2014 12:18)
Re: Otočení zlomku, odstranění logaritmu
1) Ano, záporná mocnina se přímo takto definuje:  , tedy platí
, tedy platí 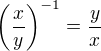 .
.
2) Ano, to je zase použití definice logaritmu – inverzní funkce k exponenciele. Platí tedy  . Jak se „zbavit“ té poloviny nám řeknou známé vzorce pro úpravu výrazů s mocninami. Konkrétně tedy fakt, že platí
. Jak se „zbavit“ té poloviny nám řeknou známé vzorce pro úpravu výrazů s mocninami. Konkrétně tedy fakt, že platí  . V tomto případě tedy
. V tomto případě tedy  .
.
Offline
#3 05. 07. 2014 12:31
#4 05. 07. 2014 12:54
Re: Otočení zlomku, odstranění logaritmu
No tou konstantou se to násobí na začátku, tak se to bude násobit i na konci. Ten výraz s e^něco jsme prostě jenom upravili na jiný tvar, takže v tom původním výrazu prostě bude vystupovat na stejném místě.
Offline
#5 05. 07. 2014 13:21
Re: Otočení zlomku, odstranění logaritmu
↑ o.neill:
Zdravím, neměla by v argumentu  být absolutní hodnota?
být absolutní hodnota?
Offline
#6 05. 07. 2014 13:31
Re: Otočení zlomku, odstranění logaritmu
↑ Sherlock:↑ Sherlock:
jj mel ale je tam důležita? To by měla "sežrat" ta konstanta pak
Offline
#7 05. 07. 2014 13:57 — Editoval o.neill (05. 07. 2014 13:58)
Re: Otočení zlomku, odstranění logaritmu
No tomu jsem nevěnoval pozornost a je to pravda, absolutní hodnota by tam měla být. To že se dá zahrnout do té konstanty je potřeba vždycky zkontrolovat. Když se výsledek napíše ve tvaru  , tak je skutečně nezbytná kvůli té odmocnině. A konstanta c pak nebude reálná, ale pouze kladná (hádám-li správně, že je to integrační konstanta, která se tam objevila při řešení lineární diferenciální rovnice). Správný výsledek tedy je
, tak je skutečně nezbytná kvůli té odmocnině. A konstanta c pak nebude reálná, ale pouze kladná (hádám-li správně, že je to integrační konstanta, která se tam objevila při řešení lineární diferenciální rovnice). Správný výsledek tedy je .
.
Je jasné, proč se znaménko nedá vyřešit tou zápornou konstantou? Jde o to, že když je 2x+1 záporné, tak to nezpůsobí to, že by byl záporný celý ten výsledek a stačilo by to vyřešit záporným c. Kvůli té odmocnině vznikne nedefinovaný výraz, protože nemůžeme odmocňovat záporná čísla.
Offline

 bude to třeba na -1?
bude to třeba na -1? 
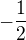 ?
?