Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Ortogonalita sdruženého a marginálního rozdělení (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 06. 2014 07:36
Ortogonalita sdruženého a marginálního rozdělení
Dobré ráno.
Nevím si rady s následujícím příkladem.
Najděte náhodný vektor  tak, aby jeho sdružené rozdělení bylo ortogonální (singulární) k součinu marginálních rozdělení náhodných veličin
tak, aby jeho sdružené rozdělení bylo ortogonální (singulární) k součinu marginálních rozdělení náhodných veličin  .
.
Budu vděčný za každou radu.
Offline
- (téma jako vyřešené označil(a) Jozef3)
#3 16. 07. 2014 20:15
Re: Ortogonalita sdruženého a marginálního rozdělení
Buď  pravděpodobnostní prostor a
pravděpodobnostní prostor a 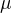 a
a 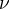 pravděpodobnostní míry na A. Pak řekneme, že
pravděpodobnostní míry na A. Pak řekneme, že 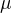 a
a 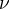 jsou ortogonální, jestliže existují disjunktní množiny
jsou ortogonální, jestliže existují disjunktní množiny  takové, že
takové, že  .
.
Doslechl jsem se, že ve spojitém případě by mělo být rozdělení náhodného vektoru ortogonální právě tehdy, když jsou jeho složky funkcionálně závislé náhodné veličiny (zajímalo by mě však zdůvodnění). V diskrétním případě je situace však složitější.
Offline
#4 17. 07. 2014 09:56
Re: Ortogonalita sdruženého a marginálního rozdělení
Pre diskretne to nepojde pre spojite sa to da napr. takto:
Uvazuj stvorec ![kopírovat do textarea $S=[0,1]\times [0,1]$](/mathtex/76/761c1dc44203477f3901ee4fb585002c.gif) a nahodny vektor
a nahodny vektor 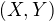 rovnomerne rozdeleny na jeho diagonale
rovnomerne rozdeleny na jeho diagonale  . Teda
. Teda  a
a  . Teraz ked si vypocitas marginalne rozdelenia, tak dostanes rovnomerne rozdelenia na intervale (intervaloch)
. Teraz ked si vypocitas marginalne rozdelenia, tak dostanes rovnomerne rozdelenia na intervale (intervaloch) ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) a teda ich sucin je rovnomerne rozdelenie na
a teda ich sucin je rovnomerne rozdelenie na  teda
teda  a
a  .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Ortogonalita sdruženého a marginálního rozdělení (TOTO TÉMA JE VYŘEŠENÉ)
