Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Práce s komplexními čísly (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 07. 2014 15:37
Práce s komplexními čísly
Ahoj, prosím Vás co se mám naučit, abych pochopil červeně zvýrazněné úpravy na obrázku.
U první případu dostanu reálnou část jako 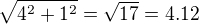
a u imaginární části získám 1.32, tak že zadám na kalkulačce při počtu v radiánech 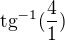
více jsem nenašel
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
- (téma jako vyřešené označil(a) Meglun)
#2 27. 07. 2014 16:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Práce s komplexními čísly
Zdravím,
potřebuješ jen převod zápisu komplexního čísla do exponenciálního tvaru (což je jen "drobná nástavba" k goniometrickému tvaru) - toto je podstatné (materiál máš?), potom jako pomocné - hodnoty pro vybrané úhly (což je převod (-1) v druhém řádku červených rámečků, pokračuješ pravidly pro násobení mocnin (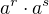 ), na závěr je záměna orientace "proti ručičkám" na opačnou
), na závěr je záměna orientace "proti ručičkám" na opačnou 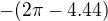 (viz "jednotková kružnice) za účelem, aby odchylka byla v rozmezí
(viz "jednotková kružnice) za účelem, aby odchylka byla v rozmezí 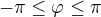 .
.
Tedy hlavně ten exponenciální tvar komplexního čísla si máš najít. Stačí tak a zbytek je již jasný? Děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Práce s komplexními čísly (TOTO TÉMA JE VYŘEŠENÉ)
