Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 08. 2014 22:20
Diferenciální rovnice-Metoda Odhadu
Dobrý den.
Chci poprosit o radu ohledně D. rovnic.Narazil jsem na zakladni příklad 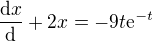
ˇřešení teto rovnice se skládá z homogenního řešení a partikulárního řešení.V čem mám problém je určení partikulárního řešení.V literatuře je uvedeno P.Ř 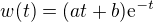
A bohužel nevím jak se mám dostat k 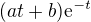
Děkuji
Offline
#2 08. 08. 2014 22:25 — Editoval Blackflower (08. 08. 2014 22:28)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Diferenciální rovnice-Metoda Odhadu
↑ Alezi: Ahoj,
ja by som povedala, že je to preto, lebo pravá strana, ktorú máš v zadaní, zodpovedá tvaru partikulárneho riešenia 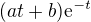 , konkrétne
, konkrétne 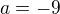 ,
, 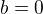 .
.
My hľadáme riešenie v obdobnom tvare, nemusí to byť zrovna to, čo som napísala, koeficienty  ,
,  by sa prípadne dourčili podľa počiatočných podmienok.
by sa prípadne dourčili podľa počiatočných podmienok.
Offline
#3 08. 08. 2014 22:40
Re: Diferenciální rovnice-Metoda Odhadu
↑ Alezi:
Ahoj,
použij hrubou sílu;-)
zderivuj:
Dosaď to do nehomogenní rovnice. Uvidíš, že exponenciálou půjde podělit obě strany rovnice, takže nebude překážet a máš rovnost polynomů. Z té už snadno dopočítáš koeficienty..
_________________________
Pokud je tvoje otázka míněna, jakým sakra kouzlem dostali ten odhad, tak to je také poměrně jednoduché. Všimni si, že pravá strana má tvar součinu polynomu a exponenciály. Představ si, co se stane, když budeš takovou funkci s polynomem stupně n derivovat:
kde P, Q, R jsou nějaké polynomy (stupně uvedeného v indexu). Tedy jinými slovy, tato funkce při derivování nemění řád toho polynomu.
Jestliže je v rovnici na pravé straně polynom stupně jedna, tak aby rovnost platila, musíš na levé straně předpokládat také polynom stupně jedna. No a pak jen určíš jeho koeficienty postupem uvedeným výše (pro rovnice vyšších řádů a pro delší polynomy je to práce jak na kostele...).
Доктор сказал «в морг» — значит в морг!
Offline
#4 09. 08. 2014 11:26
Re: Diferenciální rovnice-Metoda Odhadu
Ahoj ↑ Alezi:.
Kromě metod odhadování, zmíněných výše, lze také postupovat čistě mechanicky a použít obecný postup. Charakteristický polynom příslušné homogenní rovnice je 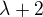 , takže homogenní řešení je
, takže homogenní řešení je 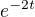 . Zbývá použít variaci konstant.
. Zbývá použít variaci konstant.
Offline
#5 09. 08. 2014 15:55
Re: Diferenciální rovnice-Metoda Odhadu
↑ Formol:
Díky za pomoc.
jestli jsem to dobře pochopil tak v uvedeném příkladě je 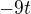 je t stupeň polynomu 1 .A proto použije
je t stupeň polynomu 1 .A proto použije 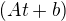
Kdyby bylo 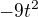 tak už je to druhý stupeň a vztah by vypadal
tak už je to druhý stupeň a vztah by vypadal 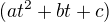
Ještě bych tě chtěl poprosit jestli by si mu trochu osvětlil výpočet hodnot 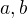
Po určení partikulárního řešení 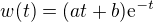 provedu derivaci w(t).
provedu derivaci w(t).
A dosadím za 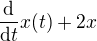
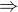
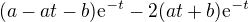
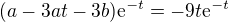
 protože vycházím z
protože vycházím z 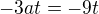 .
.
a podle řešení v publikaci 
A v tom mám další problém, nevím jak přišel na hodnotu b=1.
Offline
#7 09. 08. 2014 22:13
Re: Diferenciální rovnice-Metoda Odhadu
↑ Alezi:
Neboj se rozepisovat si výpočet krok po kroku. Těch několik vteřin a trochu více popsaného papíru ti může ušetřit hodiny hledání chyby nebo nervy z opakování zkoušky;-)
Rovnici
vydělíš exponenciálou (měl bys umět zdůvodnit, proč to můžeš udělat). Tím dostaneš:
Protože jde o rovnost polynomů, musí patit rovnost koeficientů u jednotlivých mocnin proměnné t:
Tedy soustava dvou rovnic, která má řešení a=3 a b=1.
Доктор сказал «в морг» — значит в морг!
Offline
