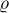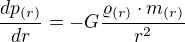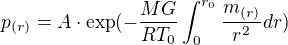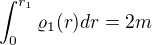Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 29. 05. 2014 19:41
Re: dva mraky
↑↑ Xellos:
Takže na tento problém je najrozumnejšie vytiahnuť numerické metódy, ak tomu správne rozumiem. Uf, to už ale nie je také exaktné. Dúfal som, že tu niekto vytiahne z rukáva riešenie :D
Neexistuje ani spôsob, ako nájsť približné riešenie?
Offline
#27 29. 05. 2014 19:46
Re: dva mraky
↑↑ Brzls:
Xellos chcel zrejme ukázať, že aj keď samotná funkcia v danom bode definovaná nie je (alebo jej limita nie je definovaná), primitívna funkcia už limitu definovanú mať môže, pričom zvolil inú funkciu m=f(r), aby to demonštroval, ale to je problém analýzy a tohto problému (dva mraky) sa netýka, nie?
Offline
#28 29. 05. 2014 19:57 — Editoval Brzls (29. 05. 2014 19:59)
Re: dva mraky
↑↑ Xellos:
Což to je pravda, když jsem to psal, tak sem nad tím moc nepřemýšlel, ale to nic nemění na tom, že ta lineární funkce není řešením původní rovnice (pro žádná r).
Pokud se nemýlím, jestli ano, chtěl bych vidět zkoušku.
↑ darkorbit:
Jo já jen neporozuměl tomu co říká...
Offline
#29 29. 05. 2014 20:22
Re: dva mraky
↑ darkorbit:
Priamo sa netyka, ale oplati sa opravit. Ten rozdiel je dost velky.
Offline
#30 29. 05. 2014 20:29
Re: dva mraky
↑ Brzls:
Nemylis sa, linearne riesenie vyhovuje len difke ktoru som napisal, ale nie samotnemu fyz. problemu (ak by bola vnutri plynu magicka prazdnota, uz by vyhovovalo :D).
↑ darkorbit:
No, naskytuju sa aproximacie ako tlak alebo rozlozenie hmotnosti odhadnut konstantne, linearne, (kvadraticke atd.) s tym ze by sa menilo len malo. Alebo skusit googlit clanky ktore by sa tomu mohli venovat, rozlozenie hmoty v gravitujucom plyne znie ako vcelku znamy problem.
Offline
#31 29. 05. 2014 20:34
Re: dva mraky
Inu mě by zajímalo jak to vidíte s poslední fází řešení, tedy jak sem zmiňoval se stanovením průměru koule po srážce a její teplotě?
Jak říkám, ze zachování energie dostaneme vztah mezi novým poloměrem a novou teplotou.
Kde vezmeme další vztah abychom měli dvě rovnice o dvou neznámých a tedy již určený konečný stav?
Offline
#32 29. 05. 2014 20:42
Re: dva mraky
↑ Brzls:
No, ak by sme mali zname rozdelenie hmoty (teda hustotu) tak to asi pojde tak ako si pisal. Osobne by som radsej robil s hmotnostou a teplotou ako polomerom a teplotou, lebo hmotnost je na rozdiel od polomeru aditivna. To nam zaroven zmaze potrebu dalsieho vztahu (pripadne by polomer a teplotu prepojila stavova rovnica).
Offline
#33 29. 05. 2014 20:53
Re: dva mraky
↑ Xellos:
Jenže poloměru se jen tak zbavit nemůžu, neboť na něm závisí konečná potenciální energie. Když se budu snažit vyjádřit tu vlastní potenciální energii, tak v integrační mezi budu mít právě poloměr a tudíž i v konečném výrazu pro energii.
Nicméně teď jsem si uvědomil, že tou druhou rovnicí bude například podmínka, že
Závislost hustoty na vzdálenosti do středu již máme teoreticky určenou právě až na teplotu (která se v jejím "zápisu" musí vyskytovat).
Teď už máme dvě rovnice o dvou neznámých a tedy i zcela určenou situaci.
Offline
#34 29. 05. 2014 21:34 — Editoval Brzls (30. 05. 2014 17:43)
Re: dva mraky
Tak tedy já osobně považuji izotermický model za teoreticky vyřešený, pro konkrétní čísla (nemyslím si, že řešení půjde vyjádřit analyticky)
Tady je soupis rovnic, které by bylo potřeba zadat do nějakého programu:
0. Značení veličin (aby nevznikali zmatky)
1. Průběh veličin v závislosti na vzdálenosti od středu
2. Stanovení energie
3. Stanovení konečného rozměru a teploty
Máte nějaké připomínky, výtky či jsou nejasnosti? Nebo se shodnem?
Offline
#35 29. 05. 2014 22:45
Re: dva mraky
↑ Brzls:
Ako si si uz uvedomil, polomer je spojeny s celkovou hmotnostou, a preto hovorim ze chceme radsej ratat s hmotnostou a teplotou, a polomer je hmotnostou nejako (mozno implicitne, mozno vztah vobec nema closed-form) dany.
Ale preco dvojka? Ratas hmotnost JEDNEHO mraku, to je skoro definicia. Preco by mal mrak mat hmotnost 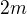 ?
?
Offline
#36 30. 05. 2014 10:19 — Editoval darkorbit (30. 05. 2014 17:08)
Re: dva mraky
↑ Brzls:
Ahoj,
s priebehom riešenia súhlasím, ale predsa mám pár nejasností. Myslím, že v Gaussovi pre gravitáciu je mínus
Potom by to mohlo robiť kladnú gravitačnú potenciálnu energiu (ktorá je úmerná 1/r, teda v nekonečne by bola nula - najvýhodnejší energetický stav a gravitácia by bola odpudivá).
Taktiež nerozumiem, ako počítaš tú pot. energiu 1 kg elementu. Vždy som takéto veci počítal tak, že som nechal gravitačnú silu si guľu poskladať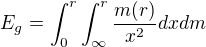
Ale je možné, že tie vyjadrenia sú ekvivalentné, každopádne sa to dá nájsť aj tu:
http://scienceworld.wolfram.com/physics … nergy.html
Inak s návrhom riešenia plne súhlasím, avšak prikláňam sa ku Xellosovi, t. j. počítať s hmotnosťou a teplotou, pretože ak nájdeme rozloženie hmotnosti, okrajové podmienky už samy vedú na rovnicu R=f(m,T), teda, tak som to skúšal s lineárnym riešením.
Pre zaujímavosť, tej difke vyhovuje aj riešenie m(r)=const, ktoré fyzikálne dáva zmysel len ak m(r)=0, teda mrak neexistuje, čo pomerne dosť zjednodušuje úlohu.
Offline
#37 30. 05. 2014 16:01 — Editoval Brzls (30. 05. 2014 16:09)
Re: dva mraky
↑ darkorbit:
↑ Xellos:
1. Jo počítat s hmotností je pohodlnější, ten poloměr jsem měl zafixovyný kvůli tomu, že sem tu úlohu před tím řešil jinak (nehledal jsem m(r) ale ro(r))
2. To 2m je tam proto, že se bavíme o mračnu PO srážce. Když se srazí dva mraky s hmotností m, tak nový mrak bude mít hmotnost 2m (jinak nevím o kterém 2m mluvíš)
3. To moje vyjádření vede ke stejnému výsledku jako v tvém odkazu, takže si myslím, že by to mělo být ekvivalentní. (nejsem si jistý jestli rozumím tomu tvému, ještě se na to kouknu)
4. ANo má tam být mínus (opravím), neboť siločáry směřují směrem ke zdroji - tok pole je záporný.
Offline
#38 30. 05. 2014 17:05 — Editoval darkorbit (30. 05. 2014 17:33)
Re: dva mraky
↑ Brzls:
Fajn, ak to tvoje vyjadrenie vedie na to, čo je v odkaze, tak potom to je úplne ok. Ja mám v tom svojom pochybne určené znamienko, tak to neber moc vážne, vedie na rovnakú absolútnu hodnotu energie, ako to tvoje - ešte to premyslím a pozmením.
Možno by nebolo od veci skúsiť celý príklad zriešiť s lineárnym riešením tej difky (myslím, že to lin. riešenie rieši aj pôvodnú rovnicu a dokonca je v zhode aj so stavovou rovnicou, aj keď si nie som istý kruhovosťou tohto dôkazu), aby sa ukázalo, či to dáva rozmerovo fajn výsledky a vôbec, bude to zaujímavejšie.
Tá vnútorná energia je určená pre dvojatómový plyn, že?
Offline
#39 30. 05. 2014 17:44
Re: dva mraky
↑ darkorbit:
Ano, pro dvouatomový. To lineární řešení ale tu původní rovnici neřeší, s tím nakonec souhlasil i Xellos.
Offline
#41 30. 05. 2014 18:09 — Editoval darkorbit (30. 05. 2014 18:10)
Re: dva mraky
Takže, postupoval som takto. Od Xellosa som vzal notáciu r_0 a limitu, ono to dosť zjednodušuje situáciu. 
Teraz dosadím to lineárne riešenie v tvare:
V exponente mi vznikne prirodzený logaritmus a exponent vyzerá takto:![kopírovat do textarea $-2\ln \frac{r}{r_{0}}=\ln [\frac{r}{r_{0}}]^{-2}$](/mathtex/67/675a22d1904620aa44611ad605e53b8f.gif)
Viem, že
Celá rovnica pre "A" potom je (pravú stranu zderivuje každý sám)
Tým je konštanta určená. Analogickým aplikovaním limity sa dá dostať k rovnici pre tlak:
Túto rovnicu môžeme odvodiť aj pomocou stavovej rovnice pre hustotu a tlak, pričom hustotu získame ako
Príde mi to ako úplne legitímny postup, ale nie som matematik, možno sa mýlim.
Inak po tých výpočtoch mi to príde, ako keby toto rozloženie hmotnosti platilo v nekonečne veľkom mraku - na krajoch nulová hustota, tlak a v strede nekonečné, teda by to mohla byť aproximácia pre "dostatočne veľký mrak".
Offline
#42 31. 05. 2014 09:31
Re: dva mraky
↑ darkorbit:
Nj, ale co je  ? Predsa nula, co znamena ze riesenie plati len ked
? Predsa nula, co znamena ze riesenie plati len ked  , resp. ze ked chceme vyratat
, resp. ze ked chceme vyratat  tak delime nulou.
tak delime nulou.
Offline
#43 31. 05. 2014 09:37
Re: dva mraky
↑ Xellos:
To vadí až tak moc? Myslel som, že takéto vyjadrenie "A" je ok a v ďalšom počítaní pre tlak tie humusy s limitou vypadnú.
Ak je to ale takto, tak postupom riešenia sme túto diskusiu zrejme ukončili.
Offline
#44 31. 05. 2014 21:14
Re: dva mraky
↑ darkorbit:
No ta rovnica urcite musi (minimalne pre fyzikalne mozne riesenia... co sa nakoniec ukaze ze toto neni) vtedy platit prave v tom limite pre  . Je mozne ze dajake veliciny budu vyjadritelne aj bez
. Je mozne ze dajake veliciny budu vyjadritelne aj bez  a netrivialne, daktore ine pojdu k nule, alebo k nekonecnu, alebo budu konecne a nenulove ale nevieme ich vyjadrit. Analyza je takychto podivnosti plna.
a netrivialne, daktore ine pojdu k nule, alebo k nekonecnu, alebo budu konecne a nenulove ale nevieme ich vyjadrit. Analyza je takychto podivnosti plna.
Offline
#45 27. 08. 2014 18:08 — Editoval Xellos (28. 08. 2014 12:07)
Re: dva mraky
Update v suvislosti s ulohou 11 z FX, ktory sa pyta v podstate na ten isty model:
1. Velky mrak nebude stabilny. (dokonca pre velky tlak nebude ani v rovnovahe)
2. Nakodil som daco, tu.
Mozte sa s tym hrat. Inak je celkom rozumne predpokladat konst. hustotu alebo aspon malo sa meniacu. Ale ked je mrak velky a kasleme na to ze IRL to tak nefunguje (sice velke mraky existuju, ale stabilizuju sa napr. magnetizmom), tak sa rozlozenie hmoty fakt blizi tomu blbemu analytickemu rieseniu (a ano, pri zvyseni teploty by sa mal zgrcnut).
Strasne velke info je v Stahler, Palla: The formation of stars (da sa to stiahnut dakde cez torrent), kapitola 2.
Offline