Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 09. 2014 16:50
Metrické úlohy v rovině
Dobrý den, vím že tímto tak trochu porušuju pravila fora tím ,že tu nemam pouze jednu úlohu. Jak si můžete všimnout dostal jsem za 5. Danou látku stále nechápu a prosil bych o podrobné vysvětlení a nějaký přehlený postup podle kterého bych to dobře spočítal.
Jsem ochoten maximálně spolupracovat abych této látce porozuměl.
Mnohokrát děkuji za vysvětlení.
Offline
#2 29. 09. 2014 17:06
- janca361

- .
- Příspěvky: 3284
Re: Metrické úlohy v rovině
↑ ander:
Ok,
1a) jak se vypočítá úhel, který svírají dva vektory (v tomto případě vektory AB a AC)?
1b) jak se vypočítá střed S úsečky AC? jak se vypočítá vzdálenost dvou bodů (SB)?
Toto je jen a pouze znalost vzorečků, druhá věc je vzorečky aplikovat
Žádám všechny kolegy, aby nepřidávali řešení dalších (pod)úloh dokud nebudou vyřešeny předcházející (pod)úlohy! Díky.
Offline
#3 29. 09. 2014 17:19
Re: Metrické úlohy v rovině
↑ janca361:
1a) 
takto
musím mít salární součin AB a AC a
a 


takto?
jak získám  a
a 
Offline
#8 30. 09. 2014 13:55
Re: Metrické úlohy v rovině
Ahoj ↑ janca361:,
Mas pravdu, ale vela tvojich stedoskolskych kolegov nepozna zapis ako A-B. ( nakmä, ze sa da obist)
(tak pre nich by bolo dat presnu definiciu toho zapisu a im dat zakladne vlasnosti o nom. ...)
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 30. 09. 2014 18:09 — Editoval vanok (30. 09. 2014 18:17)
Re: Metrické úlohy v rovině
↑ janca361:,
Staci jednoducho pouzit, ze suradnice napr.  ,
,
su  kde suradnice bodov M,N su dane vzladom k danemu suradnicovemu systemu .....
kde suradnice bodov M,N su dane vzladom k danemu suradnicovemu systemu .....
Neviem v akej miere sa vyucuju na strednych skolach aj vlasnosti v zapise ( co pouzivas) ktory sa pouziva v niektorych vysokoskolskych prednaskach afinnej geometrie.
Najlepsie by bolo vediet, ake su zdroje kolegu ↑ ander: a sa nane napasovat. No zatial nam to on nenapisal.
Dobre pokracovanie.
Kolega by nam mohol nakreslit studovanu situaciu, co by mu umoznilo sa zorientovat v rovine cvicenia.
Edit: co kolega uz vie a co nie to len on, nam moze povedat.
Niekedy staci malo, aby zrazu pochopil potrebne mechanizmy, ale akoze z tebou dobre spolupracuje, iste mu umoznis pochopit jeho medzery. A potom obaja budete mat radost z vasej spoluprace.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline


 ?
? a
a  - musíš spočítat vektor
- musíš spočítat vektor  pomocí souřadnic dvou bodů, které znáš.
pomocí souřadnic dvou bodů, které znáš.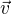 .
.