Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 10. 2014 12:33
Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy
čaute prečo sa pri definícii Baireovej triedy s ordinálnym indexom požaduje spočítateľnosť toho indexu?
jedine ak by platilo, že zjednotenie všetkých tried so spočítateľnými indexami je už vzhľadom na bodové limity uzavreté tak by nespočítateľný index nedal nič nové ak to však uzavreté nie je tak je to podľa mňa zbytočná limitácia
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 20. 10. 2014 13:17 — Editoval Rumburak (20. 10. 2014 13:21)
Re: Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy
↑ jarrro:
Ahoj.
Touto problematikou jsem se sice nikdy nezabýval do hloubky, ale také mám dojem, že proces generování
Baireových tříd se na žádném ordin. čísle nezastaví - na jedné přednášce o tom padla zmínka, pokud si dobře
pamatuji.
Offline
#3 21. 10. 2014 07:40 — Editoval jarrro (21. 10. 2014 07:40)
Re: Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy
↑ Rumburak:ahoj ďakujem potom ale nechápem prečo sa všade spomína countable ordinal transfinitná indukcia hádam funguje aj pre uncountable alebo nie?
MATH IS THE BEST!!!
Offline
#5 22. 10. 2014 10:10
Re: Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy
našiel som tento článok
možno že postačujúcosť spočítateľnosti vyplýva z toho, že Z s prvým nespočítateĺným indexom sa rovná množine svojich komplementov
nečítal som to zatiaľ nejak podrobne
MATH IS THE BEST!!!
Offline
#6 22. 10. 2014 16:20 — Editoval Rumburak (22. 10. 2014 16:26)
Re: Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy
↑ jarrro:
Do toho článku jsem sice letmo nakoukl, ale k jeho důkladnému studiu nejsem dostatečně vybaven.
Možná (ale nevím) jsou důležité i vlastnosti prostoru  , který je definičním oborem těch Baireovských
, který je definičním oborem těch Baireovských
funkcí. Ta zmínka na přednášce (viz ↑ Rumburak:) se týkala spaciálně případu  .
.
Offline
#7 22. 10. 2014 17:16
Re: Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy
↑ jarrro: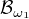 je už uzavreté na bodové limity.
je už uzavreté na bodové limity.
Dôležité je vedieť, že 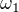 sa nedá získať ako suprémum spočítateľne veľa ordinálov. Inak povedané je to regulárny ordinál.
sa nedá získať ako suprémum spočítateľne veľa ordinálov. Inak povedané je to regulárny ordinál.
(To vlastne vyplýva z toho, že zjednotenie spočítateľne veľa spočítateľných množín je spočítateľné.)
Ak teraz máme postupnosti 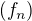 takú, že každé
takú, že každé 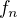 patrí do niektorej z množín
patrí do niektorej z množín  pre nejaké
pre nejaké  , tak vezmime
, tak vezmime 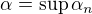 . Potom bodová limita tejto postupnosti patrí do
. Potom bodová limita tejto postupnosti patrí do  a
a  .
.
Offline
#8 23. 10. 2014 09:55 — Editoval jarrro (23. 10. 2014 10:03)
Re: Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy
↑ kompik:ahoj díky čiže spočítateľných ordinálov je spočítateľne veľa ?
platí teda  ?
?
ale keď sa tak zamyslím tak množina všetkých funkcií R do R má nejakú kardinalitu teda nemôže každý prvok indexovaného množinového systému s indexovou množinou väčšej kardinality byť neprázdny teda sa nutne musí "napúchajúca" postupnosť podmnožín množiny všetkých funkcií (je jedno či je to postupnosť baireových tried) niekde "stabilizovať"
je to tak?
MATH IS THE BEST!!!
Offline
#9 23. 10. 2014 10:08
Re: Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy
jarrro napsal(a):
↑ kompik:ahoj díky vlastne keď sa tak zamyslím tak množina všetkých funkcií R do R má nejakú kardinalitu teda nemôže každý prvok indexovaného množinového systému s indexovou množinou väčšej kardinality byť neprázdny teda sa nutne musí "napúchajúca" postupnosť podmnožín množiny všetkých funkcií (je jedno či je to postupnosť baireových tried) niekde "stabilizovať"
je to tak?
To, čo hovoríš je pravda. Čiže bol by to argument, ktorými by sme vedeli zdôvodniť, že nemôžeme mať nejaký systém  , kde by kardinalita ostro rástla. (T.j. mali by sme
, kde by kardinalita ostro rástla. (T.j. mali by sme  .)
.)
Ale v tomto prípade takýto argument nepomôže.
Vieme, že kardinalita množiny všetkých spojitých funkcií je 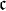 .
.
Ďalej vieme ukázať, že ak mám systém funkcií takejto kardinality a vezmem všetky ich bodové limity, dostanem opäť systém kardinality  . (Je ich nanajvýš toľko, koľko z nich viem vytvoriť postupností .)
. (Je ich nanajvýš toľko, koľko z nich viem vytvoriť postupností .)
Na základe toho indukciou dokážeme, že každá z tried, ktoré postupne vytvárame, tak každá z nich má opäť kardinalitu 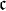 .
.
A keď to zjednotíme cez všetky ordinály menšie ako 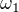 dostaneme opäť množinu kardinality
dostaneme opäť množinu kardinality 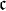 .
.
Offline
#10 23. 10. 2014 10:11
Re: Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy
jarrro napsal(a):
↑ kompik:ahoj díky čiže spočítateľných ordinálov je spočítateľne veľa ?
platí teda?
je to tak?
Vidím, že si zeditoval medzičasom svoj post, tak skúsim odpovedať ešte na to, čo pribudlo.
Nie, spočítateľných ordinálov je nespočítateľne veľa. Je ich presne  .
.
(Neviem, do akej miery ovládaš takýto prístup ku kardinálom, ale pri von Neumannovej konštrukcii sú kardinály špeciálnym prípadom ordinálov, t.j. platí 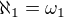 . A
. A 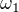 je presne množina všetkých spočítateľných ordinálov.)
je presne množina všetkých spočítateľných ordinálov.)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Bairova klasifikácia a dôvod na spočítateľnosť indexu Baireovej triedy (TOTO TÉMA JE VYŘEŠENÉ)

 ,
,