Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Integrál podílu kosinů (TOTO TÉMA JE VYŘEŠENÉ)
#1 31. 10. 2014 13:38 — Editoval inconnu (31. 10. 2014 13:39)
Integrál podílu kosinů
Zdravím,
potřeboval bych poradit s následujícím integrálem... .
.
Zkusil jsem na to jít přes následující substituci: ,
, ,
, .
.
Po postupných úpravách jsem se dopracoval k: .
.
Teď jsem se sekl.
Ale zřejmě to povede jakýmsi způsobem k použití vzorce: .
.
Jen nevím, jak se k tomu dopracovat.
Nebo se na to dá jít i (úplně) jinak???
Offline
- (téma jako vyřešené označil(a) inconnu)
#3 31. 10. 2014 15:30 — Editoval inconnu (31. 10. 2014 16:39)
Re: Integrál podílu kosinů
OK, to mi moc pomohlo, díky.
Takže ta primitivní funkce jest: .
.
No a ještě potřebuji pomoc s tímto.
Když jsem měl na začátku daný ne neurčitý, ale určitý integrál: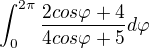 .
.
Tak nevím, jak určit:![kopírovat do textarea $[actg(tg(\frac{\varphi }{2}))+actg(\frac{1}{3}tg(\frac{\varphi }{2}))]_{\varphi =0}^{2\pi }$](/mathtex/a2/a2004405b5fd50f2a77db17281dd58a7.gif) .
.
Vůbec mi to nevychází. Má to vyjít 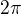 !
!
Wolfram mi to tak taky hází. ( )
)
MAW mi to však háže 0, což "je špatně".
Já sám nevím, jak to spočítat.
Tohle: 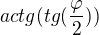 bych si možná mohl napsat pouze jako
bych si možná mohl napsat pouze jako  , ne? (Odtud bych se dopracoval k
, ne? (Odtud bych se dopracoval k 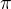 .)
.)
Ale co to "druhý"?
Když to počítám na kalkulačce nebo na netu, tak mi to háže samé nuly, takže nevím, jak se dopracovat k těm výsledným 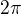 .
.
Offline
#4 31. 10. 2014 21:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál podílu kosinů
Zdravím,
↑ inconnu: podívala jsem se na historii MAW (a také na WA) - v tom může být problém s jinak zavedenou definici v jednotlivých programech (případně se sudosti/lichosti - teď ale nevidím, kde by se to projevilo). Zkusím projít ručně (ale nebude to hned) :-) Případně bychom nahlásili v místní sekci podpory MAW.
Vidí něco kolega ↑ Bati:? Děkuji.
Offline
#5 01. 11. 2014 16:14 — Editoval Bati (01. 11. 2014 16:19)
Re: Integrál podílu kosinů
↑ jelena:↑ inconnu:
Po tom částečném vydělení tam vyjde konstanta  . Tu je samozřejmě nejjednodušší zintegrovat zvlášť a dostat
. Tu je samozřejmě nejjednodušší zintegrovat zvlášť a dostat  . Pokud budeme mechanicky pokračovat ve výpočtu pomocí MAW, tahle konstanta se vrátí zpátky do zlomku a na konci logicky vyjde
. Pokud budeme mechanicky pokračovat ve výpočtu pomocí MAW, tahle konstanta se vrátí zpátky do zlomku a na konci logicky vyjde 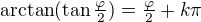 .
.
Druhý problém je v tom, že "primitivní funkce" 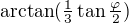 není spojitá v bodě
není spojitá v bodě  , takže zde je potřeba slepit a zde dostaneme to chybějící
, takže zde je potřeba slepit a zde dostaneme to chybějící  , neboť arkustangens "poskočí" o celý svůj obor hodnot, tedy o
, neboť arkustangens "poskočí" o celý svůj obor hodnot, tedy o  .
.
Offline
#6 01. 11. 2014 21:20
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál podílu kosinů
↑ Bati:
Zdravím a děkuji. Já jsem se dívala přímo na vložení kolegy (bez úpravy) - kde MAW dává 0. Pokud mu předložím úpravu, tak dává  (což je výsledek pro
(což je výsledek pro  (jak jsi napsal).
(jak jsi napsal).
"Kritický výsledek" je zde. Na toto se zeptám (později) v sekci CAS (kam vede podpora MAW). Spíš pokud mohu poprosit k praktickému ručnímu výpočtu:
Druhý problém je v tom, že "primitivní funkce"
není spojitá v bodě
, takže zde je potřeba slepit a zde dostaneme to chybějící
, neboť arkustangens "poskočí" o celý svůj obor hodnot, tedy o
.
pokud kolega zavede substituci  , v kterém okamžiku (a jak při výpočtu určitého integrálu) má zohlednit, že tuto substituci má pouze na
, v kterém okamžiku (a jak při výpočtu určitého integrálu) má zohlednit, že tuto substituci má pouze na ? Děkuji.
? Děkuji.
Offline
#7 01. 11. 2014 22:43
Re: Integrál podílu kosinů
↑ jelena:
Zohlednit to má tak, že si musí uvědomit, že daný výpočet primitivní funkce je korektní pouze na jistých intervalech.
Podrobněji:
Protože substituce  je definovaná pouze na intervalech
je definovaná pouze na intervalech  , musíme se při výpočtu primitivní funkce omezit na některý z těchto intervalů. Na tomto intervalu tedy provedeme daný výpočet. Je zřejmé, že tento výpočet proběhne na každém intervalu výše stejně, ovšem příslušné integrační konstanty jsou v tuto chvíli libovolné. Ze zadání víme, že existuje primitivní funkce na celém R, která musí být spojitá, takže dostáváme podmínky na integrační konstanty. Nám stačí zjistit, jak vypadá na
, musíme se při výpočtu primitivní funkce omezit na některý z těchto intervalů. Na tomto intervalu tedy provedeme daný výpočet. Je zřejmé, že tento výpočet proběhne na každém intervalu výše stejně, ovšem příslušné integrační konstanty jsou v tuto chvíli libovolné. Ze zadání víme, že existuje primitivní funkce na celém R, která musí být spojitá, takže dostáváme podmínky na integrační konstanty. Nám stačí zjistit, jak vypadá na 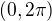 , proto stačí spočítat jednostranné limity v bodě
, proto stačí spočítat jednostranné limity v bodě  a spojitě napojit.
a spojitě napojit.
Offline
#9 01. 11. 2014 23:37
Re: Integrál podílu kosinů
↑ inconnu:
Na  mi vyjde primitivní funkce
mi vyjde primitivní funkce 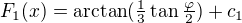 , na
, na  pak
pak  . Platí
. Platí  ,
,  . Zvolím-li např.
. Zvolím-li např. 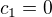 a
a  , pak tyto funkce "na sebe napojím" a tuhle spojenou funkci nazvu primitivní funkci na celém
, pak tyto funkce "na sebe napojím" a tuhle spojenou funkci nazvu primitivní funkci na celém  .
.
Říká se tomu "lepení", pojem "spojité napojování" je zavádějící, protože nám nezáleží na hodnotě funkce v napojovaném bodě, ale jen na jejím chování v okolí.
Offline
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Integrál podílu kosinů (TOTO TÉMA JE VYŘEŠENÉ)

 a
a  , ne?
, ne?