Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 05. 11. 2014 17:16
Re: Derivace funkce
↑ dry92:
Vypocital jsem jiz nekolik desitek prikladu s derivaci a nemel jsem problem, ale proste u techto dvou jsem se zasekl. Clovek obcas potrebuje nakopnout a chyti se. Nepatrim mezi ty osoby, ktere si sem davaji komplet domaci ukol, ale jdu sem, jen kdyz proste nevim.
Tento komentar mi fakt nepomohl.
Offline
#4 05. 11. 2014 17:37 — Editoval bonifax (05. 11. 2014 17:38)
Re: Derivace funkce
Ahoj A1,
jsou to složené funkce, u obou příkladů použiješ vzorec pro derivaci složené funkce
V prvním příkladě to bude následovně:
1. použití vzorce pro složenou funkci a derivaci exponencionální funkce
2. zkrácení
Příklad 2)
podobně, použiješ vzorec pro derivaci složené funkce.


Offline
#5 06. 11. 2014 11:34 — Editoval RadekHampl (07. 11. 2014 08:11)
- RadekHampl

- Místo: Varnsdorf
- Příspěvky: 32
- Škola: FSv ČVUT, abs. 95 a 09
- Pozice: ---
- Reputace: 3
Re: Derivace funkce
Jen pro lepší pochopení, abychom jen nederivovali pomocí vzorců, [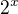 ]´ =
]´ = 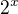 .ln(2) se odvodí z tzv. logaritmického derivování. Jde o to, že logaritmus je definována takto:
.ln(2) se odvodí z tzv. logaritmického derivování. Jde o to, že logaritmus je definována takto:
y = ln(x) <=>  = x
= x
a odtud  .
.
Takže  .
.
No a potom v derivaci to vypadá takto: ![kopírovat do textarea $[2^{x}]^\prime = [e^{ln(2^{x})}]^\prime = [e^{x.ln(2)}]^\prime=e^{x.ln(2)}.ln(2) = 2^{x}.ln(2)$](/mathtex/5d/5d0918efca0489b0500e192d79ecc911.gif)
No a tohle taky můžeš použít, když si uvědomíš, že: 
a dále už jen to logaritmický derivování.
Podobně ten druhý příklad...
Offline
#6 06. 11. 2014 11:35 — Editoval RadekHampl (07. 11. 2014 14:30) Příspěvek uživatele RadekHampl byl skryt uživatelem RadekHampl. Důvod: uvedeno výše na jednom řádku...
#7 06. 11. 2014 11:37
- RadekHampl

- Místo: Varnsdorf
- Příspěvky: 32
- Škola: FSv ČVUT, abs. 95 a 09
- Pozice: ---
- Reputace: 3
Re: Derivace funkce
Zobrazení derivace nějak hapruje, ale to už dáš dokupy sám...
Offline
#8 06. 11. 2014 20:28 — Editoval A1+ (06. 11. 2014 20:33)
Re: Derivace funkce

Pánové, děkuji Vám oběma za podanou pomocnou ruku. U prvního příkladu mám díky Vám zcela jasno. U druhého jsem postupoval správně z hlediska derivací, ale opakovaně jsem dělal chybu v následné algebraické části. Teď jsem si ji našel :)
Offline
#9 07. 11. 2014 00:20
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace funkce
Zdravím,
↑ RadekHampl:
pro zápis derivace - dovolím si citovat pár typofrafických připomínek :-). Potom "nehapruje" (jinak "haprování" je třeba nahlašovat).
↑ A1+: to je dobře, že se všechno našlo, pro kontrolu postupu lze také používat MAW. Označím za vyřešené.
Offline
#10 07. 11. 2014 07:31
- RadekHampl

- Místo: Varnsdorf
- Příspěvky: 32
- Škola: FSv ČVUT, abs. 95 a 09
- Pozice: ---
- Reputace: 3
Re: Derivace funkce
↑ jelena:
no ten méně vhodný zápis jsem nepoužil, vždy značka derivace byla mimo závorek i když připouštím, použil jsem ' . Ale jinak děkuji, budu spíše volit prime...
A dále děkuji za upozornění na nahlašování, nejsem tu dlouho (respektive jsem se tu dlouho zase neukázal), tak mi některé povinnosti unikly. Mrknu na to...
Offline






