Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Ortogonizační proces (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 11. 2014 11:18
- janca361

- .
- Příspěvky: 3284
Ortogonizační proces
Zdravím,
mám následující příklad:
Najděte pomocí Gramm-Schmidtova ortogonalizačního procesu ortogonální bázi podprostoru 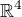 generovaného vektory
generovaného vektory 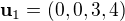 ,
,  ,
, 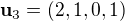 . Vyjděte ze zadaného pořadí vektorů, výsledné vektory nenormujte.
. Vyjděte ze zadaného pořadí vektorů, výsledné vektory nenormujte.
Dokázala jsem správně určit 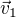 a
a 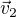 ,
, 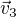 mi nevychází.
mi nevychází.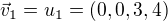
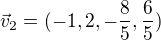

Má platit: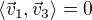
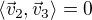



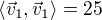


Co s tím  , dopočítat stejně jako
, dopočítat stejně jako  , z
, z 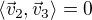 ?
?
Předem díky za pomoc.
Offline
- (téma jako vyřešené označil(a) janca361)
#2 17. 11. 2014 13:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Ortogonizační proces
Zdravím,
ano, měla bys ještě počítat ještě z 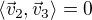 koeficient
koeficient  (jelikož ve výpočtu se objevuji nové vektory báze, o kterých víš, že jsou kolmé, tak tato dvojice ve skalárním součinu "vynuluje" svůj koeficient). Výpočty jsem nekontrolovala, ale tu jsme s kolegou cvičili využití WA pro takové úlohy, možná něco použiješ pro kontrolu.
(jelikož ve výpočtu se objevuji nové vektory báze, o kterých víš, že jsou kolmé, tak tato dvojice ve skalárním součinu "vynuluje" svůj koeficient). Výpočty jsem nekontrolovala, ale tu jsme s kolegou cvičili využití WA pro takové úlohy, možná něco použiješ pro kontrolu.
Ozvi se, jak se vede.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Ortogonizační proces (TOTO TÉMA JE VYŘEŠENÉ)