Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#6 04. 12. 2014 20:10
Re: obor hodnôt
↑ BielečkaB:A pri funkcii typu  to vies? Tam je to lahke. A tvoja funkcia sa na nieco take da upravit.
to vies? Tam je to lahke. A tvoja funkcia sa na nieco take da upravit.
Offline
#7 04. 12. 2014 20:24
Re: obor hodnôt
↑ vlado_bb: No v tej funkcii si viem vyjadriť  a z toho viem že y sa nesmie rovnať 2. Teda ak som použil správnu metódu.
a z toho viem že y sa nesmie rovnať 2. Teda ak som použil správnu metódu.
Problém je že nevidím ako upraviť ten môj zlomok na taký tvar a čo na tom zmení ta absolútna hodnota.
Offline
#9 04. 12. 2014 20:45
Re: obor hodnôt
↑ vlado_bb: Určite mi mala pomôcť tá úprava? Po použití toho vzťahu som dostal  čo mi moc nepomohlo. Resp. možno malo ale stále mám problém si z toho vyjadriť funkciu pre x a určiť podmienku pre y.
čo mi moc nepomohlo. Resp. možno malo ale stále mám problém si z toho vyjadriť funkciu pre x a určiť podmienku pre y.
Offline


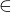 (-
(- , -3/2)
, -3/2)  <0 ,
<0 ,  .
. a dalej podla mojho navodu.
a dalej podla mojho navodu.