Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 12. 2014 19:33
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Integrál
Ahoj, už si nevím rady s integrálem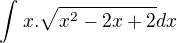
vypadá triviálně, ale o to je složitější. Zkoušel jsem Eulerovy substituce, ale dostal jsem strašně složité výrazy. Mohl by prosím někdo poradit? Dík
Offline
#2 09. 12. 2014 20:18
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Integrál
Našel jsem jen výsledek:
I = 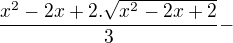
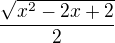
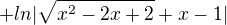
Offline
#3 09. 12. 2014 20:23
Re: Integrál
↑ Argcotgh x:
Zdravím.
Nic 'moudrého' mě nenapadá, jenom úprava a substituce![kopírovat do textarea $\int x\cdot \sqrt{x^2-2x+2}\,dx=\int\left[(x-1)\sqrt{(x-1)^2+1)}+\sqrt{(x-1)^2+1)}\right]\,d(x-1)=$](/mathtex/d8/d8f4ea1231b77a3a545dc4e09d0f7f43.gif)
![kopírovat do textarea $=\int\left[t\sqrt{t^2+1)}+\sqrt{t^2+1)}\right]\,dt$](/mathtex/75/759dc7bde2c150f2f307bf87e3cbb9e0.gif)
což bude asi o kapánek jednoddušší.
Pokud se tedy nemýlím.
Offline
#5 09. 12. 2014 20:31
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Integrál
Díky moc za inspiraci, snad to pomůže.
Zapomněl jsem na jeden člen, ten výsledek má být správně: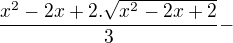
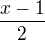
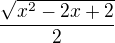
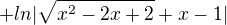
Offline
#6 09. 12. 2014 20:34
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Integrál
Ahoj Bati, ty poslední dva integrály ani nemusím počítat, ty znám z hlavy :-) i ten s \sqrt{1+x^2}, jsou naprosto triviální.
Teď jde už jen o to, jestli je postup substituce správný.
Offline
#7 09. 12. 2014 22:47
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Integrál
Taxem to spočítal a dosadil a skutečně to vyjde !!! Netušil jsem, že na to zafunguje tak jednoduchá metoda. Díky moc !!!
Akorát u toho členu s logaritmem mi před ním vychází koeficient 1/2, ale to je asi numerická chyba.
Jinak při výpočtu integrálu 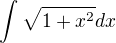
je užitečné vědět vztah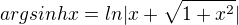
Offline
#8 09. 12. 2014 22:57
Offline