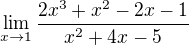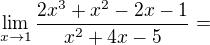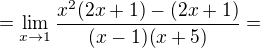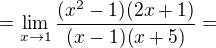Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 12. 12. 2014 23:09
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Limita
Nejdřív vydělíš čitatele jmenovatelem - algoritmus dělení polynomu polynomem.
Dostaneš 2x - 7 - (36 x - 36)/(x^2 + 4x - 5) neboli 2x - 7 - 36 . (x-1)/(x^2 +4x -5)
Protože kvadratický trojčlen x^2 - 4x + 5 má dva reálné kořeny, 1 a (-5), lze jej rozložit na (x-1)*(x+5)
Teď můžeme vykrátit
x - 1 1
__________ = ____
(x-1)*(x+5) x+5
Celkem dostáváme 2*1 - 7*1 - 36 / (1+5) = 2 - 7 - 6 = - 11
Takhle nějak by to mělo vyjít, pokud jsem někde neudělal numerickou chybu.
Offline
#3 12. 12. 2014 23:17
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Limita
To dělení polynomu polynomem:
2 x^3 + x^2 - 2x - 1 : x^2 + 4x - 5 = 2x - 7 + (36x-36)/(x^2 + 4x - 5)
-2x^3 - 8x^2+10x
7x^2+8x -1
- 7x^2+28x-35
36x-36
Offline
#5 12. 12. 2014 23:31
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Limita
Aha, udělal jsem numerickou chybu - má být
2*1 - 7*1 + 36 / (1+5) = 2 - 7 + 6 = 1
teď je to správně.
Offline