Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nalezení lim sup (n-->∞) a lim inf (n-->∞)
#1 02. 01. 2015 13:31
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Nalezení lim sup (n-->∞) a lim inf (n-->∞)
Zdravím, mohl bych poprosit o nápovědu k tomuto příkladu? Ještě jsme to neprobírali, tudíž nemám představu o řešení.
Nalezněte lim sup (n-->∞) a lim inf (n-->∞)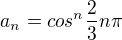
Offline
#2 02. 01. 2015 15:07 — Editoval Bati (02. 01. 2015 15:27)
Re: Nalezení lim sup (n-->∞) a lim inf (n-->∞)
↑ Argcotgh x:
Ahoj,
limsup by měla být jasná, vezmi podposloupnost 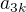 .
.
A co se týče liminf, stačí si rozmyslet k čemu konvergují ty ostatní podposloupnosti.
Offline
#3 02. 01. 2015 15:35
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Nalezení lim sup (n-->∞) a lim inf (n-->∞)
Bohužel mi to moc jasné není :-( předchází se nám cvičení před přednáškou...
Offline
#4 02. 01. 2015 15:41
Re: Nalezení lim sup (n-->∞) a lim inf (n-->∞)
↑ Argcotgh x:
Začni tím, že určíš 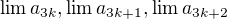 , pokud existují.
, pokud existují.
Offline
#5 02. 01. 2015 15:59
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Nalezení lim sup (n-->∞) a lim inf (n-->∞)
Napadá mě, že když zvolím n = 3k, dostanu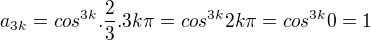
vlastně 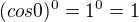
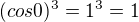
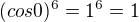
atd.
Offline
#6 02. 01. 2015 16:08
Re: Nalezení lim sup (n-->∞) a lim inf (n-->∞)
↑ Argcotgh x:
Takže si našel podposloupnost, která má limitu 1. Je ale zřejmé, že zadaná posloupnost je omezená shora jedničkou, z čehož už plyne závěr pro limsup (buď z tvrzení, že limsup se dá realizovat jako obyčejná limita nějaké podposloupnosti, anebo přímo z definice).
Co ty ostatní?
Offline
#7 02. 01. 2015 17:11
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Nalezení lim sup (n-->∞) a lim inf (n-->∞)
Ty ostatní jsou horší:
3k+1: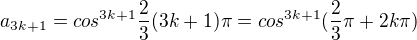
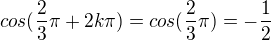
ale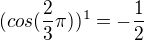
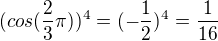
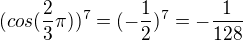
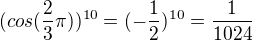
atd.
takže to znaménkově osciluje, ale přijde mi, že s rostoucím "k" to jde k nule
Podobně
3k+2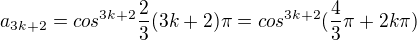
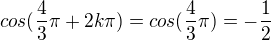
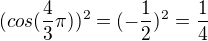
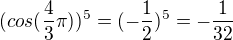
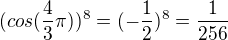
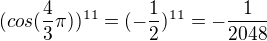
atd.
takže to taky znaménkově osciluje, ale taky mi přijde, že s rostoucím "k" to jde k nule.
Offline
#9 02. 01. 2015 18:03
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Nalezení lim sup (n-->∞) a lim inf (n-->∞)
Právě že mi není jasný ten důkaz a závěr :-(
Offline
#10 02. 01. 2015 18:19 — Editoval Bati (02. 01. 2015 18:20)
Re: Nalezení lim sup (n-->∞) a lim inf (n-->∞)
↑ Argcotgh x:
Ten důkaz nulovosti limit jsem udělal v první části mého předchozího příspěvku, uvědom si, že 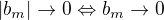 ,
, 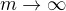 ).
).
S tím liminf...napiš definici a urči ty jednotlivá infima.
Offline
#11 04. 01. 2015 16:15
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Nalezení lim sup (n-->∞) a lim inf (n-->∞)
Bohužel mi to stále není jasné...nebyla by ještě nápověda?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nalezení lim sup (n-->∞) a lim inf (n-->∞)

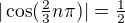 , pokud
, pokud 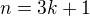 nebo
nebo 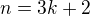 . Zřejmě ale
. Zřejmě ale 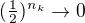 pro
pro  .
.