Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 01. 2015 20:04
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Analytika v rovině
Zdravím, už se pěknou chvilku trápím s jedním příkladem a nemůžu ho rozlousknout.. Prosím o pomoc.
Zadání zní: Najděte všechny body C takové, že leží na přímce p: x-y-2=0 a trojúhelník ABC má obsah = 1. A[3,4], B[2,5].
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
- (téma jako vyřešené označil(a) jelinekgreen)
#2 04. 01. 2015 20:41
Re: Analytika v rovině
↑ jelinekgreen:
Dobrý den. Obsah trojúhelníka o vrcholech A(3,4), B(3,5) a C(x,y) můžeme vyjádřit např. jako absolutní hodnotu determinantu:
Takže bych řekl, že z rovnice
můžeme spočítat x-ové souřadnice hledaných vrcholů C, k nim příslušné y-ové souřadnice dopočítat z rovnice dané přímky.
Pokud se tedy nemýlím.
Offline
#3 04. 01. 2015 20:58
Re: Analytika v rovině
Ahoj,
obsah trojúhelníku je polovina obsahu rovnoběžníku. Obsah rovnoběžníku je dán vzorcem: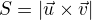 kde vektory u a v představují jeho nerovnoběžné strany.
kde vektory u a v představují jeho nerovnoběžné strany.
Hledáš tedy bod ![kopírovat do textarea $C[c_1;c_2]$](/mathtex/4f/4f6ce4573d99efbed67c541ac5cb4538.gif)
Jeden vektor již znáš 
druhý vektor bude obsahovat neznámou: 
Uděláš vektorový součin těchto dvou vektorů a velikost tohoto vektoru položíš 1. Nakonec vyjádříš c1 nebo c2 pomocí rovnice přímky, na které daný bod leží a dopočítáš zbylé výsledky..
Postup přes matice je ovšem též korektní, ale přijde mi že determinant u typu 3x3 je početně daleko delší.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 04. 01. 2015 21:36
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#5 04. 01. 2015 21:39 — Editoval Freedy (04. 01. 2015 22:46)
Re: Analytika v rovině
↑ jelinekgreen:
a co ti brání si za tu třetí souřadnici dosadit v obou případech 0? Kdybychom to osekali, tak je pak obsah trojúhelníku, jehož dvě strany jsou vektory u a v roven:
Edit: ano, jedna polovina tam skutečně je.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 04. 01. 2015 21:48
- misaH
- Příspěvky: 13431
Re: Analytika v rovině
↑ jelinekgreen:
To chodíš do matematickej triedy, keď rátate determinanty?
Offline
#8 04. 01. 2015 21:49
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
↑ Jj:
Tento výpočet mi vyhodil graficky odpovídající řešení. (asi - těžko se to odhaduje..) Ale řešení existují každopádně 2 a nevím, kde v tomhle postupu narazit na nějaké plus/minus...
Ale každopádně děkuju :)
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#9 04. 01. 2015 21:51
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
↑ misaH:
Do prváku na výšce, ale tohle mi přišlo středoškolské. Teda až na ten fakt, že mi to nejde :D Ale doufal jsem v jednodušší postup. Resp. já se dopracoval k druhému výsledku středoškolsky, ale taky tam nevidím prostor pro získání druhého bodu C
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#10 04. 01. 2015 22:00 — Editoval misaH (04. 01. 2015 22:01)
- misaH
- Příspěvky: 13431
Re: Analytika v rovině
↑ jelinekgreen:
Aha.
Freedy má s tým obsahom pravdu.
Ja by som to robila úplne natvrdo.
Zistila vzdialenosť AB, vyrátala výšku trojuholníka z obsahu a zistila rovnice rovnobežiek s AB v príslušnej vzdialenosti.
No a priesečníky rovnobežiek s danou priamkou.
Ale je to zdĺhavé a asi ozaj existujú omnoho elegantnejšie riešenia.
Offline
#11 04. 01. 2015 22:06
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
↑ Freedy:
Pokud dosadím za zetové souřadnice nulu. Bude nula i ve třetím řádku/třetím sloupci determinantu a tím pádem dostanu 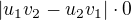 ?
?
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#12 04. 01. 2015 22:41
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
Tadyhle jsem ofotil dva postupy. Jeden od Jj a spodní ode mně. Každý ale spočítá jen jeden ze dvou správných postupů. Zajímalo by mě, kde v těch postupech, ty opačné výsledky ztratily. Při testu nebude čas nad tím takhle hluboce hloubat a uvažovat, který výpočet vypustí jaký výsledek :/
http://postimg.org/image/6cvfe4fdb/
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#13 04. 01. 2015 22:44
Re: Analytika v rovině
Ahoj, je smutné, že někdo, kdo pracuje s maticemi, ani netuší, jak vypadá vektorový součin. Nicméně, hodně zdaru při počítání s maticemi, když vůbec netušíš jak fungují, tak je potom zbytečné s nimi počítat.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#14 04. 01. 2015 22:55
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
↑ Freedy:
My jsme si vektorový součin definovali takto: http://postimg.org/image/439gzdr6x/
Mně na první pohled připadá, že dosazením za zetové souřadnice se na místě "k" objeví nula. Ale je samozřejmě možné, že se pletu. Vlastně právě proto se tady ptám! A jestli je něco smutného, tak ne to, že já něčemu nerozumím, ale že tobě to stojí za posměšek.
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#15 04. 01. 2015 23:03
Re: Analytika v rovině
Dobře, tak to můžeme zkusit jinak. Co to je vektorový součin? Jaký vektor vznikne vektorovým součinem dvou nekolineárních vektorů?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#16 04. 01. 2015 23:09
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
↑ Freedy:
Pro mě je to číslo, které získám jako determinant matice - viz odkaz. Vektorovým součinem vznikne nový vektor, kolmý na oba původní.
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#17 04. 01. 2015 23:11
Re: Analytika v rovině
V tom případě, jak může být z-ová souřadnice nulová, jestliže tento vektor má být kolmý na dva vektory ležící v rovině z = 0 ?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#18 04. 01. 2015 23:22 — Editoval jelinekgreen (04. 01. 2015 23:24)
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
To nemůže.. Ale přemýšlím, jak to teda povyplňovat ten determinant. Resp. jestliže je výsledkem vektor v=(i,j,k), tak vyjde  ?
?
A velikost tohoto vektoru tedy položím rovnu jedné?
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#19 04. 01. 2015 23:35 — Editoval Freedy (04. 01. 2015 23:44)
Re: Analytika v rovině
Nevím, já se do matic nebudu pouštět.
Já znám vektorový součin jako:
Ty máš body [3,4] a [2,5] a přímku x-y-2=0 a hledáš bod C[c1,c2] tak, aby byl obsah trojúhelníku ABC 1.
Vektor 
Vektor 
vektorový součin  po vynásobení -1 dostáváme:
po vynásobení -1 dostáváme: 
velikost tohoto vektoru je:
ta velikost má být rovna 1 tudíž: po umocnění
po umocnění
Bod ![kopírovat do textarea $C[c_1,c_2]$](/mathtex/00/009bd81e8bb23f06f048b1c6c9c9d52f.gif) leží na přímce x - y - 2 = 0. Tudíž platí
leží na přímce x - y - 2 = 0. Tudíž platí  . Dosadíš do rovnosti výše a dostáváš:
. Dosadíš do rovnosti výše a dostáváš: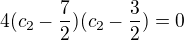
a tedy

PS: děkuji za zápornou reputaci.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#20 05. 01. 2015 00:01
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
↑ Freedy:
Jo. Chápu. Díky moc :)) Přece jenom jsem bojoval s tím vektorovým součinem. Tam se musí ještě za ty i/j/k dosadit orty a pak se to převede teprve na konečný vektor.. Každopádně ani teď na mě tenhle případ nepůsobí úplně triviálně.
Akorát ještě: můžu postupovat takto? 
Tenhle postup mi vyhodí sice správný výsledek, ale zase jen jeden. Kde přesně se tam, prosím, ten druhý výsledek ztrácí?
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
#22 05. 01. 2015 00:18
- jelinekgreen

- Příspěvky: 168
- Reputace: 0
Re: Analytika v rovině
↑ misaH:
Ano, já jsem potom uvažoval  , akorát že jsem tam udělal početní chybu a dostal se tak na stejný výsledek. Takhle už získávám oba. A přijde mi to teda poměrně jednodušší.
, akorát že jsem tam udělal početní chybu a dostal se tak na stejný výsledek. Takhle už získávám oba. A přijde mi to teda poměrně jednodušší.
Takže ještě jednou všem moc děkuji za pomoc :)
Fyzika je jako sex, může mít i praktické výsledky, to ale není to, proč to děláme.
Offline
