Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Exponenciální a logaritmická funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 03. 2009 19:43 — Editoval lauralee (10. 03. 2009 20:17)
Exponenciální a logaritmická funkce
Prosím, mohl by mi někdo pomoct s následujícími příklady?
1) Nalezněte primitivní funkce k daným funkcím:
a) y=sinx + 4/x; (0;+ nekonečno)
b) y=2e na xtou; R
2) Najděte definiční obor, intervaly monotónnosti a lokální extrémy funkcí:
a) y=2-e na xtou + xe
b) y=x-lnx
3) Vypočítejte plochu útvaru ohraničeného křivkami:
y=3/x; y=4-x
4) Dokažte, že daná rovnice má právě jedno řešení a určete toto řešení:
x=1+lnx
Moc díky všem.
Offline
#2 10. 03. 2009 19:51 — Editoval Olin (10. 03. 2009 19:52)
Re: Exponenciální a logaritmická funkce
Pomoct bychom určitě mohli, ale je toho docela dost, takže by bylo fajn, kdybys nějak naznačil(a), co konkrétně ti vlastně dělá problémy, kam ses dostal(a) atd. Tady to derivování, integrování atd. je dost mechanická činnost, navíc tyto příklady nejsou nijak složité.
Udělám 1 a):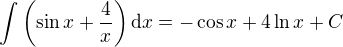
Do logaritmu nemusím dát absolutní hodnoty, protože x je pouze kladné podle zadání.
Všechno, co jsem použil, jsou naprosto základní vzorce pro integrování.
Ještě upozorňuji, že to, co zadáváš ve čtyřce, rozhodně rovnice není…
Offline
#3 10. 03. 2009 20:10
Re: Exponenciální a logaritmická funkce
↑ Olin:
Díky za výpočet, co se týče 4. př., to nám zadala naše učitelka na matematiku a tak to stálo v zadání, jen jsem to opsala, takže nevím. Já toho z integrací a derivací moc neumím, snad jenom vzorečky dokážu použít. Z matematiky nematuruji a ani ji nebudu potřebovat na VŠ, a navíc jsem téď déle chyběla, takže opravdu ani trochu nevím, co s tím. Takže kdybys měl (třeba i za pár dní) čas a chuť některé další z těch příkladů vypočítat, moc by mi to pomohlo. Nebo by mi alespoň stačilo naznačit, co s tím - např. udělej první derivaci, zintegruj atd. Ještě jednou díky za ten 1. příklad. Lauralee
Offline
#4 10. 03. 2009 21:16 — Editoval jelena (10. 03. 2009 21:49)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Exponenciální a logaritmická funkce
↑ Olin:
Zdravím :-)
Editace (omluva pro Olina): byla jsem upozorněna kolegou lukaszh(em)(skloňuji), že když jsi psal tento příspěvek, tak to nebyla rovnice a teď :
4) rovnice to je
Řešila bych graficky - nakreslim graf - přímku y=x (nebo po přesunu 1 nalevo y=x-1) a graf funkce y=1+lnx (nebo y=lnx). A prokážu, že společný bod je pouze jeden.
↑ lauralee:
Zdravím :-)
2) Najděte definiční obor, intervaly monotónnosti a lokální extrémy funkcí:
a) y=2-e na xtou + xe
b) y=x-lnx
Budeš potřebovat najit:
def. obory pro a) jsou to R, pro b) (0, +oo)
derivace (podle vzorců, jak umíš):
položit derivace rovne 0 a vypočítat hodnotu x, kde se to stane - budou to body podezřelé z extrému, pomocí ověření znaménka derivace před a po podezřelém bodu (pokud derivace při přechodu přes bod změní znaménko), potvrdit, že jsou to extrémy.
Vysvětleno: http://www.mojeskola.cz/Vyuka/Php/Learn … rokem4.php
3) Vypočítejte plochu útvaru ohraničeného křivkami:
y=3/x; y=4-x
Stačí nakreslit zadané grafy (první - nepřímá úměra, druhý přímka, najit x-souřadnici průsečíků - společných bodů grafů a vypočítat určitý integrál.
Vysvětleno: http://www.mojeskola.cz/Vyuka/Php/Learn … rokem7.php
Pokud se nepodaří - tak se ozví tady. Hodně zdaru :-)
Offline
#5 10. 03. 2009 21:27
#6 10. 03. 2009 21:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Exponenciální a logaritmická funkce
↑ lukaszh:
Zdravím a děkuji - no bylo mi to zvláštní, že kolega Olin něco takového hlasí :-)
půjdu editovat....
Offline
#7 10. 03. 2009 22:39 — Editoval Olin (10. 03. 2009 22:42)
Re: Exponenciální a logaritmická funkce
Ohledně té rovnice 4)
Předpokládám, že se to chce řešit nějak takto:
převedeme na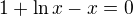
Následně ukážeme, že funkce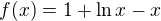
je na intervalu 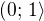 rostoucí, v
rostoucí, v 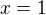 má maximum a na intervalu
má maximum a na intervalu  je klesající. Z toho plyne, že má rovnice právě jedno řešení, a to
je klesající. Z toho plyne, že má rovnice právě jedno řešení, a to 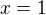 (protože
(protože  ).
).
Offline
#8 13. 03. 2009 20:44
Re: Exponenciální a logaritmická funkce
děkuji všem za výpočty, s tou rovnicí se omlouvám, místo = jsem zadala omylem - a nevšimla si toho, takže jsem nevěděla, jak to uživatel Olin myslí, proč to není rovnice - matematika totiž není moje silná stránka(-:, ale všimla jsem si toho až později, tak jsem to - předělala na =, zkrátka předtím to opravdu nebyla rovnice (-:
Offline
#9 13. 03. 2009 22:36
Re: Exponenciální a logaritmická funkce
U trojky je nutné udělat si obrázek a zjistit průsečíky obou funkcí. Výsledná plocha pak bude integrál z "horní" funkce (mezemi jsou průsečíky) mínus integrál z "dolní" funkce. To plyne z toho, že když je funkce nezáporná, tak je integrál z té funkce roven obsahu plochy pod křivkou.
Protože průsečíky jsou v bodech 1 a 3 (x-ové souřadnice), bude výsledný obsah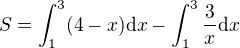
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Exponenciální a logaritmická funkce (TOTO TÉMA JE VYŘEŠENÉ)
