Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 19. 01. 2015 14:35 — Editoval blak (19. 01. 2015 16:57)
Re: Lagrangeovi multiplikátory
Zkusím to dosadit do g1, jestli vyleze správný výsledek.
Edit:
Teda smekám před Vámi Paní/slečno Jeleno za vaši trpělivost se mnou. Teď to skutečně vyšlo. Moc děkuju, teď už vím, že i když nejvyjde klasická 1:1 rovnice 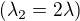 , tak se s tím má počítat a ne si dělat hlavu, že mi to zase nevychází :)
, tak se s tím má počítat a ne si dělat hlavu, že mi to zase nevychází :)
Offline
#27 19. 01. 2015 16:28
Re: Lagrangeovi multiplikátory
Zdravím v tematu.
Jen tak pro kontrolu můžeme úlohu vyřešit následující úvahou:
Funkce  , jejíž extrémy hledáme, je druhou mocninou vzdálenosti bodu
, jejíž extrémy hledáme, je druhou mocninou vzdálenosti bodu ![kopírovat do textarea $[x, y, z]$](/mathtex/87/87ddee431967292cd6c973dae9cb128f.gif)
od počátku.
Rovnicemi  ,
,  jsou určeny plochy, jejichž průnikem je jistá elipsa se středem
jsou určeny plochy, jejichž průnikem je jistá elipsa se středem
v počátku.
Extrémy funkce  vzhledem k této elipse tedy budou v jejích vrcholech. Pokud to už objevil někdo jiný,
vzhledem k této elipse tedy budou v jejích vrcholech. Pokud to už objevil někdo jiný,
tak se omlouvám - příspěvků je zde hodně a nestíhám přečíst všëchno. Časem snad se dostanu i k L. metodě.
Offline
#28 19. 01. 2015 20:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
↑ blak:
děkuji, to je dobře, že vyšlo a ještě lépe, že se zvýšilo odhodlání :-) "Paní Jelena" bude ideální - připomíná mi to a tam se všem říkalo "paní", jelikož děj probíhal v polské kavárně.
↑ Rumburak: děkuji velice. Elipsu jsem, tuším, objevila (ale za cenu ztráty  ), tak nevím, zda ten objev byl k užitku.
), tak nevím, zda ten objev byl k užitku.
kolega Rumburak napsal(a):
Časem snad se dostanu i k L. metodě.
to vůbec nespěchá, jak vyjde čas a nálada (nejde přímo o LM přes 2 lambdy, tu jsem přepočetla a překontrolovala, v tom problém není), ale o možnost/nemožnost dosazovat jednu z vazeb do zadaní funkce (nebo vazbu do vazby).
A pozdrav.
Offline
#29 20. 01. 2015 10:56 — Editoval Rumburak (20. 01. 2015 15:17)
Re: Lagrangeovi multiplikátory
↑ jelena:
Dle pokynu zdravím :-) .
Takže pro ![kopírovat do textarea $X = [x, y, z]$](/mathtex/96/964117be9e5b18ac3bd24ab0bbbe0d05.gif) máme funkce
máme funkce
 ,
,
 ,
,

a hledáme extrémy funkce  vázané podmínkami
vázané podmínkami
(0)  ,
,  .
.
Budeme potřebovat gradienty uvedených funkcí:
(1)  ,
,
(2)  ,
,
(3)  .
.
Z věty o L.m. vyplývá: nachází-li se hledaný vázaný extrém v bodě ![kopírovat do textarea $X = [x, y, z]$](/mathtex/96/964117be9e5b18ac3bd24ab0bbbe0d05.gif) , potom vektory
, potom vektory
(1), (2), (3) jsou lineárně závislé, takže čtvercová matice 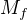 , jejímiž řádky jsou tyto vektory, má
, jejímiž řádky jsou tyto vektory, má
determinant rovný 0. K rovnicím (0) tak získáváme třetí rovnici pro neznámé  .
.
Tento postup mi zde připadá výhodnější než pracovat přímo s multiplikátory. Vyšlo mi:
minimum v bodech ![kopírovat do textarea $[ 3 , -1 , 0] , [-3 , 1 , 0]$](/mathtex/6d/6d1515906eda8e880ea277c552e25798.gif) ,
,
maximum v bodech ![kopírovat do textarea $[ 1 , 3 , 2] , [ -1 , -3 , -2] $](/mathtex/2d/2da6a837e47e4189b8ea9ca04fb7260a.gif) .
.
K alternativnímu postupu, když do předpisu funkce  dosadíme vazební podmínku s funkcí
dosadíme vazební podmínku s funkcí  :
:
Hledáme tedy extrémy funkce 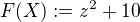 pří týchž vazbách. Nyní je
pří týchž vazbách. Nyní je 
a tomu odpovídající matice 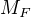 bude mít řádky
bude mít řádky
(1')  ,
,
(2')  ,
,
(3')  .
.
Snadno nahlédneme, že determinanty matic  jsou si rovny.
jsou si rovny.
Dosazovat vazbu do funkce (a řekl bych, že i vazbu do vazby) můžeme, ala s tou dosazenou vazbou
(v naší úloze s vazbou  ) musíme zacházet úplně stejně, jako kdyby k dosazení nedošlo.
) musíme zacházet úplně stejně, jako kdyby k dosazení nedošlo.
Například domnívat se , že se dosazením sníží počet multiplikátorů, by bylo chybou.
Offline
#30 20. 01. 2015 22:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
kolega Rumburak napsal(a):
Dle pokynu
:-) dostáváš růžový puntík a v celoročním hodnocení bude zohledněno. Ale tamto byl můj pozdrav, který s potěšením zopakuji, že pozdrav a děkuji velice.
Děkuji za podrobný rozbor, to mi zcela uniklo, že z geometrického pohledu (a nejen) se také mohu podívat na gradient (přitom v metodách to bývá). Doufám, že i kolega příspěvek podrobně projde, je to o hodně úspornější metoda (i když technikou, řeknu, srovnatelná s využitím Jakobiánu).
Také děkuji k vysvětlení k vazbám - samotné dosazování mi nepřišlo "zakázané", ale, že nejde tak snížit počet multiplikátorů, to budu brát jako fakt (doplním i poznámku do předchozích příspěvku, kde používám). Sice mi pořád není zcela jasné, jak vysvětlit i v geometrickém smyslu (ale to by ani pořádně nešlo, byla bych svou představou omezena v 3D).
Offline
#32 21. 01. 2015 10:02
Re: Lagrangeovi multiplikátory
Zdravím,
Já to prostudoval, ale nějak nechápu o co se Rumburak snažil, za to můžou ty čáry máry ;) Vzhledem k tomu, že já podle zadané fce nepoznám o jaký geo. tvar jde, tak ani nechápu to vysvětlení. Nicméně jsem na ten příklad už přišel a kdyby někoho zajímalo, proč mi to nevycházelo, tak šlo o mou "numerickou" chybu s mezerou, že jde o vzorec :(
Offline
#33 21. 01. 2015 13:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
Zdravím,
↑ Rumburak: děkuji, já jen mám trošku potíž si odůvodnit - dosazením vazby do zadání funkce provádím řez plochy definované předpisem funkce řezem plochy definované vazbou, tedy si tak v 3D vytvořím jejich společnou křivku a na této křivce vyšetřuji extrém s ohledem na druhou vazbu, která už (pokud jde) vyznačí bod. Obdobně bych si "představovala" i výš, než 3D, že spojením vazby a funkce mi vzniká nová "jednodušší" funkce, kterou budu vyšetřovat.
Jen to nějak mi není jasné, proč pořád musím uvažovat i tu použitou vazbu. Ale mé "trošku potíž" není žádná potíž: mně stačí, když se řekne, že tak je chybně :-)
↑ blak: možná projít např. tento materiál (nebo upřesnit, zda by nebyl odkaz na váš materiál - 2 vazby je např. specifikum VŠE z mého pozorování). Jinak přenechám debatu kolegovi Rumburakovi (to bude mít větší efekt). Také samozřejmě záleží, jak moc v tomto zkouškovém období máš prostoru na podrobnější seznámení.
Pokud píšeš, že už úlohy vycházejí a jsou spíš numerické chyby, tak už je to dobrý posun oproti úvodu tématu.
Offline
#34 21. 01. 2015 14:57 — Editoval Rumburak (21. 01. 2015 16:18)
Re: Lagrangeovi multiplikátory
↑ jelena:
Také zdravím.
Jen to nějak mi není jasné, proč pořád musím uvažovat i tu použitou vazbu.
Přiznám se, že Tvá úvaha mne na chvíli zviklala, takže jsem si to raději přepočítal:
Hledejme tedy pro změnu extrémy funkce  s vazbou
s vazbou  .
.
Metodou L. m. dostáváme rovnici 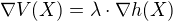 platnou pro vhodné
platnou pro vhodné  , tedy
, tedy , odtud
, odtud  ,
,  libovolná (třeba i splňijící
libovolná (třeba i splňijící  ).
).
Problém vidím v tom, že dosazením vazby do funkce , jejíž extrémy hledáme, dojde obecně ke změně této funkce
(geometricky řečeno jejího grafu) v bodech nevyhovujících vazbě, což by nevadilo, pokud bychom s dosazenou vazbou
počítali i nadále v plném rozsahu daném větou o L. m. Ale když ji vynecháme "z výpočtu" podle této věty, pak dostaneme
výsledek takový, jako kdybychom hledali extrémy (pozměněné funkce) přes POZMĚNĚNOU MNOŽINU.
Když ale ve výpočtu vazbu uplatníme, zůstane vše v pořádku, protože body, v nichž funkce byla pozměněna, budou
vyloučeny ze hry.
Offline
#35 21. 01. 2015 16:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
↑ Rumburak:
děkuji, to jsem neměla v plánu viklat. Ale musíš uznat, že ten dopad je takový nečekaný (nebo, co je horší - maskovaný, jelikož část bodů jsme našli).
Tedy jednoznačně:
Když ale ve výpočtu vazbu uplatníme, zůstane vše v pořádku, protože body, v nichž funkce byla pozměněna, budou
vyloučeny ze hry.
Děkuji za téma.
Offline
#36 23. 01. 2015 11:06 — Editoval blak (23. 01. 2015 12:55)
Re: Lagrangeovi multiplikátory
Rumburak mohl by jsi mi rozepsat jak si přišel k řešení minima (-3,1,0) s multiplikátory ? Já to stále nechápu, dořešil jsem jen to maximum, ale nezbylo mi nic, jak vyjádřit minimum :(
Já se k minimu dostal jen způsobem od Jeleny s dosazením jedné vazby do zadání a pak už s ní dál nepočítal. Takhle mi minimum vyšlo, ale nevyšlo zas maximum.
Edit: Já se k minimu a maximu dostal jen Jacobiánem, ale zajímala by mě ta cesta pomocí LM, abych viděl, kde je zakopaný pes. Přeci jen test se blíží a rozvádět tam dva způsoby je časově náročné.
Offline
#37 23. 01. 2015 13:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
Zdravím,
↑ blak: kolega Rumburak v předchozích příspěvcích došel k závěru, že dosazovat vazbu můžeme, ale stejně musí být zahrnuta i v LM (tedy pořád budeme mít 2 lambdy, jen snad ten výpočet může být rychlejší.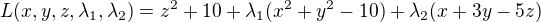 zůstává. Pokud jsem počítala dobře, tak z prvních řádů (derivace po x, po y) dostaneš
zůstává. Pokud jsem počítala dobře, tak z prvních řádů (derivace po x, po y) dostaneš 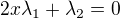
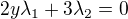
sečtením a úpravou máme součin  , který je dobře použitelný pro další výpočty. Překontroluj ale, prosím.
, který je dobře použitelný pro další výpočty. Překontroluj ale, prosím.
Offline
#38 23. 01. 2015 16:03 — Editoval Rumburak (23. 01. 2015 16:09)
Re: Lagrangeovi multiplikátory
↑ blak:
Pro ![kopírovat do textarea $X = [x, y, z]$](/mathtex/96/964117be9e5b18ac3bd24ab0bbbe0d05.gif) máme funkce
máme funkce
 ,
,
(1)  ,
,
(2) 
a hledáme extrémy funkce  při vazebních podmínkách
při vazebních podmínkách  . Jak již bylo vysvětleno,
. Jak již bylo vysvětleno,
tentýž výsledek dostaneme, když při zachování vazebních podmínek nahradíme funkci  funkcí
funkcí 
získanou z  dosazením první vazební podmínky. Podle věty o L.m. pak hledáme čísla
dosazením první vazební podmínky. Podle věty o L.m. pak hledáme čísla  taková, aby
taková, aby ,
,  ,
,  .
.
Odtud  a tedy
a tedy  , z posledních dvou rovnic máme
, z posledních dvou rovnic máme
(*)  .
.
Další postup se větví na dvba případy:
I.  , tedy i
, tedy i  a zbývající souřadnice hledaného kandidáta na extrém vypočteme ze soustavy
a zbývající souřadnice hledaného kandidáta na extrém vypočteme ze soustavy
 plynoucí z vazebních podmínek.
plynoucí z vazebních podmínek.
II. 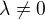 . Ze soustavy (*) vyjádříme
. Ze soustavy (*) vyjádříme  a dosadíme do vazebních podmínek.
a dosadíme do vazebních podmínek.
Z podmínky (1) pak vyplyne 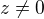 , takže rovnici
, takže rovnici  plynoucí z (2) můžeme
plynoucí z (2) můžeme
vydělit proměnnou  a dostaneme rovnici již s jedinou neznámou
a dostaneme rovnici již s jedinou neznámou  . Atd. - to jsi zvádl, jak soudím z dotazu.
. Atd. - to jsi zvádl, jak soudím z dotazu.
Offline
