Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 20. 01. 2015 17:35
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Kanonická báze
Taky se jí říká standardní báze. Objevuje se všude možně. Výhoda je, že souřadnice vektoru z 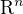 vzhledem ke kanonick bázi jsou přímo příslušné složky vektoru.
vzhledem ke kanonick bázi jsou přímo příslušné složky vektoru.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#5 20. 01. 2015 17:46
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Kanonická báze
↑ TGar: Kanonická je výhradně ta báze v  , kde její i-tý vektor má ve všech složkách nulu a na i-tém místě jedničku. Ortonormální může být i jiná báze, třeba v
, kde její i-tý vektor má ve všech složkách nulu a na i-tém místě jedničku. Ortonormální může být i jiná báze, třeba v  máme kromě nekonečně mnoha jiných ortonormálních bází také ortonormální bázi
máme kromě nekonečně mnoha jiných ortonormálních bází také ortonormální bázi 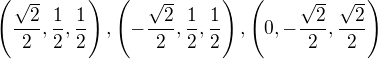 .
.
Tedy předpokládám, že metrika je euklidovská.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#6 20. 01. 2015 17:47
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Kanonická báze
↑ TGar: Bacha, máš stejně označenou bázi i prostor :-). Ty všechny podmínky musí platit nutně jen pro bázové vektory, ne všechny vektory v prostoru.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#7 20. 01. 2015 17:50
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Kanonická báze
Jinak Google, dotaz "kanonická báze definice" a asi třetí odkaz.
http://www.math.muni.cz/~kadourek/bazedim.pdf
Anebo mnou zmiňované učebnice lineární algebry od L. Bicana nebo J. Bečváře.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
 to je
to je 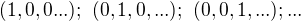
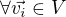 platí
platí 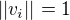 a současně
a současně 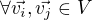 platí
platí 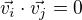 .
.