Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Podmínka při integraci (TOTO TÉMA JE VYŘEŠENÉ)
#3 25. 01. 2015 13:30
Re: Podmínka při integraci
↑ maver:Ide o definicny obor primitivnej funkcie. Tu je ale ina zaludnost. To, co je v poslednom riadku, nie je primitivna funkcia k funkcii pod integralom. Prinajmenej treba komentar, na ktory by som sa ta na mieste skusajuceho urcite opytal. Vsimni si, na akom type mnozin sa hovori o primitivnej funkcii.
Offline
#4 25. 01. 2015 14:24 — Editoval maver (25. 01. 2015 14:26)
Re: Podmínka při integraci
↑ Freedy:
Takže podle Freedyho jde o zkoumání podmínky zadání.
Je to tak dobře?
Pozn. Nejde mi o určení podmínky pro x (jde o vyřešený příklad). Jde mi o to, na jakém výrazu mám zkoumat podmínku.
Takže prosím odpověď v tomto formátu:
Podmínku pro x zkoumám na
a) pouze počátečním výrazu (zadání)
b) pouze na výsledku
c) podmínka pro x se určuje jak podle výsledku tak i na zadání
Děkuji.
PS: podmínka primitivní funkce je její spojitost, ne?
Offline
#5 25. 01. 2015 14:33 — Editoval vlado_bb (25. 01. 2015 14:34)
Re: Podmínka při integraci
↑ maver:Primitivna funkcia k  na intervale
na intervale  je taka funkcia
je taka funkcia  , ze pre kazde
, ze pre kazde 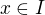 je
je  . Tym je vec vyriesena, staci teraz iba uvazovat, ci moze existavat
. Tym je vec vyriesena, staci teraz iba uvazovat, ci moze existavat  tam, kde nie je
tam, kde nie je  definovana a ci ma
definovana a ci ma  primitivnu aj inde ako na definicnom obore
primitivnu aj inde ako na definicnom obore  . Zaroven je tym vyriesena aj podstatna vec, ktoru som spominal vyssie.
. Zaroven je tym vyriesena aj podstatna vec, ktoru som spominal vyssie.
Prepac, ze nedodrziavam predpisany format odpovede.
Offline
#6 25. 01. 2015 14:52 — Editoval maver (25. 01. 2015 14:57)
Re: Podmínka při integraci
↑ vlado_bb:
nestuduji teoretickou matematiku, ale informatiku, proto požaduji pouze formátovanou odpověď.
Ale něco mi říká, že c) je správně. Takže průnik.
Offline
#8 25. 01. 2015 15:17
Re: Podmínka při integraci
↑ vlado_bb:
Tento příklad je plně okopírován z vyřešených učebních textů z FIT.CVUT.CZ
Nechci být papežtější, než papež, chápete, že ...
Offline
#10 25. 01. 2015 15:51
Re: Podmínka při integraci
↑ vlado_bb:
já právě ne, ale rozumím obecnému zadání = podmínka pro zadání i výsledek .. a z toho odvodím výslednou podmínku.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Podmínka při integraci (TOTO TÉMA JE VYŘEŠENÉ)


 . V ulohach ako tato je podstatny.
. V ulohach ako tato je podstatny.