Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 01. 2015 22:22
Užití derivace
Dobrý večer,
měl bych otázku k následujícímu příkladu níže. Nejprve by mne však zajímalo, jak vůbec takováto funkce vlastně bude vypadat.
Předem děkuji.
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
- (téma jako vyřešené označil(a) Flaky)
#2 26. 01. 2015 22:27
Re: Užití derivace
↑ Flaky:
Hezký večer,
stačí si celou funkci přepsat tak, jak bude vypadat na intervalech (-infty,2], (2,3] a (3,+infty). Pak se z té kabaly vyloupne docela slušný zápis, kde bude třeba pouze vyšetřit chování v bodech 2 a 3.
Доктор сказал «в морг» — значит в морг!
Offline
#4 26. 01. 2015 22:42
Re: Užití derivace
no, když si to rozdělím na tyto intervaly, tak např. v intervalu 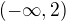 bude funkce max brát stále hodnotu 3 a funkce minimum vždy dané x na intervalu? Dělá mi problém si ty funkce jakoby spojit dohromady.
bude funkce max brát stále hodnotu 3 a funkce minimum vždy dané x na intervalu? Dělá mi problém si ty funkce jakoby spojit dohromady.
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline

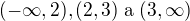 . Měla by zmizet ta maxima a minima. Pak bude jasný průběh funkce a snad i zbylé dotazy.
. Měla by zmizet ta maxima a minima. Pak bude jasný průběh funkce a snad i zbylé dotazy.