Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 03. 2009 19:42 — Editoval joker (13. 03. 2009 19:58)
Směrnice přímky
Zdravím a prosím o kontrolu :-]
Zadání:
Směrnice přímky, která prochází středy kružnice k1 a k2 kde: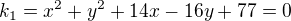
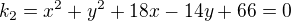
je rovna číslu...
Moje řešení:
Kružnice převedu na středové rovnice a zjistim souřadnice středů: ![kopírovat do textarea $S_1=[-7;8]$](/mathtex/f0/f08db556b7220c70e787d1ff3ef9cf22.gif)
![kopírovat do textarea $S_2=[-9;7]$](/mathtex/13/1340658435b7543c5d283e92e2c845ed.gif)
Znám tedy dva body přímky, mohu si zjistit směrový vektor a z něj normálový:
Nápišu obecnou rovnici přímky a dosadím: 
...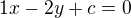
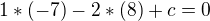
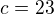
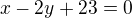
Převedu na směrnicový tvar přímky:
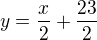
Směrnice přímky je rovna jedné polovině 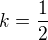
Offline
