Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 01. 2015 18:47 — Editoval Pavel (28. 01. 2015 20:55)
Odmocnina z matice
Existuje reálná regulární matice  taková, že maticová rovnice
taková, že maticová rovnice
kde  je neznámá reálná matice, má nekonečně mnoho řešení?
je neznámá reálná matice, má nekonečně mnoho řešení?
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
- (téma jako vyřešené označil(a) Pavel)
#2 28. 01. 2015 20:26
Re: Odmocnina z matice
Ahoj ↑ Pavel:,
Iste sa zaujimas o riesenie tvojho problemu na telesach  .
.
Je jednoduche ukazat ze ak  je riesenie problemu, tak
je riesenie problemu, tak  a
a  komutuju. A preto sa daju triangolizovat v tej istej baze.
komutuju. A preto sa daju triangolizovat v tej istej baze.
Porozmyslaj trochu o tom. Vratim sa k tomuto zaujimavemu problemu ked budem mat viac casu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 28. 01. 2015 20:54
Re: Odmocnina z matice
↑ vanok:
Veškeré úvahy by se měly odehrávat v 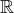 , raději upřesním zadání. Já řešení mám, jinak díky za tip.
, raději upřesním zadání. Já řešení mám, jinak díky za tip.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 28. 01. 2015 21:06 — Editoval kafe_arabica (28. 01. 2015 21:25)
- kafe_arabica
- Příspěvky: 38
- Reputace: 3
Re: Odmocnina z matice
Ahoj.
Nie som si úplne istý, lebo to je veľmi rýchle ...
Keďže A je regulárna, teda aj invertovateľná, musí byť X invertovateľná. Z toho, ide o matice rovnakej dimenzie. Pohybujeme sa v grupe invertovateľných prvkov. Tieto tvoria banachovu algebru B. Z vety (Geľfand - Mazur), B je izometricky izomorfná  . Teda tú rovnicu môžeme uvažovať v
. Teda tú rovnicu môžeme uvažovať v  , kvôli tomu izomorfizmu. V
, kvôli tomu izomorfizmu. V  má dve riešenia.
má dve riešenia.
Edit: Ja som uvažoval komplexnú algebru. No mohlo by sa to dať nejako vyladiť.
Edit2: Vyladenie. S tými komplexnými číslami by nemal byť problém. Uvazujem algebru reálnych regulárnych matíc so skalármi komplexnými číslami.
Offline
#5 28. 01. 2015 21:40
Re: Odmocnina z matice
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 28. 01. 2015 21:42
- kafe_arabica
- Příspěvky: 38
- Reputace: 3
Re: Odmocnina z matice
Môžeš to trochu rozvinúť, prečo to je problém?
Offline
#7 28. 01. 2015 21:45
Re: Odmocnina z matice
↑ kafe_arabica:
Problém je v tom, že těch řešení existuje občas více než 2.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 28. 01. 2015 23:54
Re: Odmocnina z matice
Offline
#9 29. 01. 2015 07:46 — Editoval Pavel (29. 01. 2015 10:54)
Re: Odmocnina z matice
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#10 29. 01. 2015 10:42
- kafe_arabica
- Příspěvky: 38
- Reputace: 3
Re: Odmocnina z matice
Dalo by sa k tomu niečo viac povedať? Prekvapilo ma, že to má viacej ako 2 riešenia. Nerieši takéto záležitosti nejaká teória? Resp., nejaká/é veta/y ohľadom tohto.
Offline
#11 29. 01. 2015 10:56 — Editoval Pavel (29. 01. 2015 10:57)
Re: Odmocnina z matice
↑ kafe_arabica:
Bohužel do teorie matic až tak moc nevidím. Problém vyplynul zcela náhodou při psaní cvičebnice pro studenty. Možná by se k tomu mohl vyslovit někdo povolanější.
Ke svému řešení jsem doplnil ještě jednu zajímavou poznámku.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#12 29. 01. 2015 16:28
- check_drummer

- Příspěvky: 5182
- Reputace: 106
Re: Odmocnina z matice
Ahoj, dalo by se cvičení zobecnit a charakterizovat všechny takové matice A?
"Máte úhel beta." "No to nemám."
Offline
#13 29. 01. 2015 18:44 — Editoval Pavel (29. 01. 2015 18:46)
Re: Odmocnina z matice
↑ check_drummer:
Úloha byla určena pro studenty 1. ročníku a vedla na nalezení řešení maticové rovnice 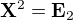 , kde
, kde  je jednotková matice 2. stupně.
je jednotková matice 2. stupně.
Bude-li  reálná čtvercová matice 2. stupně, tak obdobné výsledky lze obdržet, bude-li
reálná čtvercová matice 2. stupně, tak obdobné výsledky lze obdržet, bude-li  diagonální a její determinant bude kladný.
diagonální a její determinant bude kladný.
Je zřejmé, že nutná podmínka existence řešení maticové rovnice  je, aby matice
je, aby matice  měla nezáporný determinant.
měla nezáporný determinant.
Dále lze ukázat, že má-li matice  všechny své čtyři prvky nenulové a má-li kladný determinant, pak rovnice
všechny své čtyři prvky nenulové a má-li kladný determinant, pak rovnice  může mít buď 2 nebo 4 řešení.
může mít buď 2 nebo 4 řešení.
Pro vyšší stupně matice bude charakterizace určitě komplikovanější, podrobnosti neznám. Bude to určitě souviset s maticovými funkcemi, což má spojitost vlastními čísly a vektory, charakteristickými polynomy apod.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#14 29. 01. 2015 19:23
Re: Odmocnina z matice
↑ Pavel:,
Pridavat este malu poznamku.
Ak sa limitujeme na involucie (ktore su vlastne symétrie, v pripade lin. aplikacii) tak pridavam toto citanie http://en.m.wikipedia.org/wiki/Involutory_matrix
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline


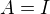 , kde
, kde  je jednotková matica. Nech
je jednotková matica. Nech 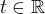 je ľubovolné, potom zadaný problém splňujú matice
je ľubovolné, potom zadaný problém splňujú matice .
. je matica
je matica  , preto uvažujeme práve symetrické ortogonálne matice.
, preto uvažujeme práve symetrické ortogonálne matice. 
 jsou libovolná reálná čísla, pro která platí
jsou libovolná reálná čísla, pro která platí  . Pak lze všechna reálná řešení maticové rovnice vyjádřit ve tvaru
. Pak lze všechna reálná řešení maticové rovnice vyjádřit ve tvaru
